VROA intensities of methyloxirane

Here we show an example of how to calculate the VROA intensities of methyloxirane calculated with an incident wavelength of 488.9 nm.

Run the VROA code

First import any packages that we need. Mainly just need the VROA class from vibrav.

from vibrav.base import resource
from vibrav import VROA
import numpy as np

Initialize the class and print the elements in the configuration file

with open(resource('methyloxirane-vroa-va.conf'), 'r') as fn:
    print(fn.read())

DELTA_FILE                    methyloxirane-vroa-delta.dat.xz
SMATRIX_FILE                  methyloxirane-vroa-smatrix.dat.xz
ATOM_ORDER_FILE               methyloxirane-vroa-atom_order.dat.xz
REDUCED_MASS_FILE             methyloxirane-vroa-redmass.dat.xz
FREQUENCY_FILE                methyloxirane-vroa-freq.dat.xz
EQCOORD_FILE                  methyloxirane-vroa-eqcoord.dat.xz
ROA_FILE                      methyloxirane-vroa-roa.csv.xz
GRAD_FILE                     methyloxirane-vroa-grad.csv.xz
NUMBER_OF_MODES               24
NUMBER_OF_NUCLEI              10
USE_RESOURCE                  1

vroa = VROA(config_file=resource('methyloxirane-vroa-va.conf'))

Run the vroa method to calculate the intensities. Internally we read the ROA and gradient data from the lines in the configuration file corresponding to roa_file and grad_file. These have to be created prior to the run and are simple csv files generated by the python library, pandas.

For more information about how we parse the outputs you can refer to the tutorial on parsing the NWChem outputs using exatomic.

vroa.vroa()

Print the VROA intensities and other pertinent information

vroa.scatter

	freq	freqdx	beta_g*1e6	beta_A*1e6	alpha_g*1e6	backscatter	forwardscatter	exc_freq	exc_idx
0	200.247393	0	3.656216	-0.273074	0.040271	0.000342	0.000092	488.9	0
1	354.450962	1	-35.948619	-4.790522	-0.202244	-0.003604	-0.000644	488.9	0
2	398.589617	2	2.472626	4.730142	-1.325064	0.000389	-0.000990	488.9	0
3	719.359726	3	132.090769	38.915333	2.796307	0.013926	0.003504	488.9	0
4	798.974164	4	-170.470297	-21.596906	-1.259120	-0.017056	-0.003289	488.9	0
5	875.765502	5	-179.496773	-85.647522	0.856508	-0.019972	-0.000885	488.9	0
6	930.279028	6	43.652907	13.460119	4.053168	0.004621	0.003401	488.9	0
7	1007.463980	7	42.888944	22.644693	1.396536	0.004842	0.001329	488.9	0
8	1090.810610	8	-20.942816	-10.046244	-1.407385	-0.002332	-0.001188	488.9	0
9	1111.217660	9	111.839344	10.336868	0.211851	0.011067	0.001777	488.9	0
10	1124.140810	10	11.552339	13.400895	-0.161749	0.001538	-0.000146	488.9	0
11	1149.661160	11	-115.650502	-30.017963	2.671025	-0.012063	0.000553	488.9	0
12	1248.157950	12	50.434903	-3.105703	-7.331371	0.004742	-0.004422	488.9	0
13	1370.356780	13	15.428338	-8.882977	-0.118462	0.001197	0.000304	488.9	0
14	1389.679630	14	-56.263793	-25.389564	-5.371933	-0.006214	-0.004362	488.9	0
15	1447.995300	15	-108.852976	-9.084926	-0.441561	-0.010741	-0.001914	488.9	0
16	1462.169630	16	270.411325	92.294289	-0.617040	0.028913	0.002406	488.9	0
17	1484.006190	17	-79.691973	-11.972509	0.002530	-0.008034	-0.001082	488.9	0
18	2955.233120	18	-135.170825	38.082939	-28.831868	-0.011758	-0.023531	488.9	0
19	2996.254680	19	979.837908	-38.224550	49.152893	0.092841	0.051679	488.9	0
20	3003.433440	20	-1954.768108	-415.801685	-60.440709	-0.200963	-0.068141	488.9	0
21	3006.058620	21	-260.461289	-480.375629	5.705709	-0.040376	0.007627	488.9	0
22	3031.862470	22	783.244711	360.553324	-23.132314	0.086729	-0.009892	488.9	0
23	3074.662670	23	490.996556	303.938290	40.039345	0.056862	0.031821	488.9	0

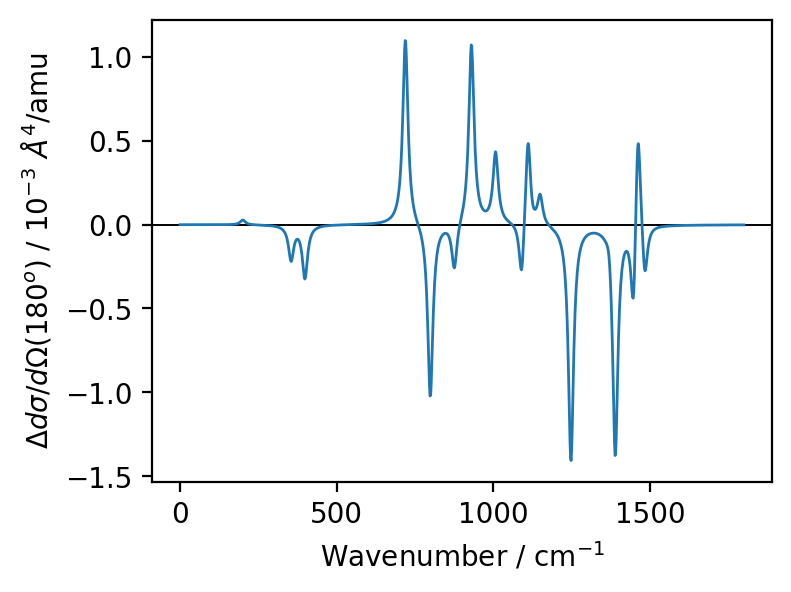
Plot the calculated intensities

We use a full-width at half-maximum of 20 wavenumbers.

For this example we use ‘atomic’ units where the calculated VROA units are in \(\unicode{xC5}^4/\text{amu}\)

Set up the lineshape function

def lorentz(omega, omega_0, fwhm):
    return (1/np.pi) * 05.*fwhm / ((omega-omega_0)**2 + 0.25*fwhm**2)

x = np.linspace(0, 1800, 1000)
y = np.zeros(1000)
arr = zip(vroa.scatter['freq'], vroa.scatter['forwardscatter'])
for omega_0, inten in arr:
    y += lorentz(omega=x, omega_0=omega_0, fwhm=20)*inten

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(4,3), dpi=200)
ax = fig.add_subplot(111)
ax.axhline(0, color='k', linewidth=0.7)
ax.plot(x, 1e3*y, linewidth=1.0)
ax.set_xlabel('Wavenumber / cm$^{-1}$')
ax.set_ylabel(r"$\Delta d\sigma/d\Omega\left(180^{o}\right)$ / $10^{-3}~\AA^{4}$/amu")
plt.show()