Introduction#
In this notebook I am using the housing data set from Ames, Iowa (can be found on Kaggle) where I will be performing:
[2]:
from matplotlib import ticker
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
import os
import warnings
warnings.filterwarnings("ignore")
[66]:
def missing_vals(df):
'''
Get the number and percentage of missing values per column in
the given data frame.
Args:
df (pandas.DataFrame): Data frame with the data.
Returns:
null_df (pandas.DataFrame): Data frame consisting of two
columns, 'count' and 'percent', representing the number
and percentage of columns missing in the data frame,
respectively. The index will be the column names.
Will only return columns that are missing values. If
there are no missing values it will return an empty
data frame.
'''
null_vals = df.isnull().sum(axis=0)
null_vals = null_vals[null_vals > 0].sort_values(ascending=False).rename('count')
null_perc = null_vals / df.shape[0] * 100
null_perc.name = 'percent'
null_df = pd.concat([null_vals, null_perc], axis=1)
return null_df
def calc_iqr(arr):
per = np.percentile(arr, [25, 75])
iqr = per[1] - per[0]
return per, iqr
def get_iqr_vals(df):
per, iqr = calc_iqr(df['SalePrice'].values)
tmp = df.loc[(df['SalePrice'] < per[0] - 1.5*iqr) | (df['SalePrice'] > per[1] + 1.5*iqr), 'SalePrice']
return tmp.count()
def do_loop(idx1, idx2, msg):
''' Helper function for ensuring all the columns have a description '''
for i in idx1:
is_missing = True
for j in idx2:
if i == j:
is_missing = False
break
if is_missing:
print(msg.format(i))
def compare_feature_keys(keys, columns):
''' Helper function for column descriptions '''
print("Keys missing in description")
do_loop(columns, keys, " - Missing key {} in description")
print("Keys missing in description")
do_loop(keys, columns, " - Missing key {} in data set")
def highlight_max(s, props=''):
import numpy as np
return np.where(s == np.nanmax(s.values), props, '')
def gen_cat_matrix(df, x, y, fill=0, color='tab:blue', linewidth=0.9):
'''
Generate a heatmap representation of the number of values in a set
of categorical columns. Uses the heatmap function in seaborn.
Args:
df (pandas.DataFrame): Data frame with the pertinent data. This
can be the complete data frame or a slice.
x (str): Column name that will be used as the x-axis in the
heatmap plot.
y (str): Column name that will be used as the y-axis in the
heatmap plot.
fill (int, default=0): Number to use for filling in missing
values when making the pivot table.
color (str, default='tab:blue'): Color to use for the box lines.
linewidth (float, default=0.9): Linewidth for the box lines.
'''
import seaborn as sns
tmp = df.groupby([x, y])[y].value_counts().reset_index()
pivot = pd.pivot_table(data=tmp, index=x, columns=y, values='count').fillna(fill).astype(int)
# sns.heatmap(pivot, annot=True, fmt='.0f', linecolor=color,
# linewidth=linewidth)
p = pivot.style
p.highlight_max(props='color:white;background-color:darkblue', axis=1)
# p.set_properties(**{'text-align': 'center'})
p.set_table_styles([
{'selector': 'th:not(.index_name)', 'props': 'background-color: #000066; color: white; text-align: center'},
{'selector': 'td', 'props': 'text-align:center; font-weight: bold;'},
])
p.set_properties(**{'width': '100px'})
return p
def fill_mode(sr):
''' Function to calculate the mode and fill in missing values. '''
mode = sr.dropna().agg(pd.Series.mode)
return sr.fillna(mode[0])
def replace_price_ticks(ax, xaxis, label='Price'):
'''
Replace the plot ticks in the given plot with hard-coded values
determined for our purpose.
Note:
This will create axis ticks spaced every 10e3 units and set
the tick labels to be in units of thousands.
Args:
ax (matplotlib.axis.Axes): Matplotlib Axes object.
xaxis (bool): Set that we are replacing the xaxis ticks.
label (str, default='Price'): Label preceeding the units.
'''
ticks = np.arange(0, 9e5, 1e5)
labels = [str(int(round(t/1e3,0))) for t in ticks]
if xaxis:
ax.set_xticks(ticks, labels)
ax.set_xlabel(f'{label} / 10$^3\\times$USD')
else:
ax.set_yticks(ticks, labels)
ax.set_ylabel(f'{label} / 10$^3\\times$USD')
def gen_lotfront_plot(df, group_cols):
'''
Function to visualize how the replacement that we make for the missing
values in the 'LotFrontage' column will affect the overall values. We
generate a plot for the effect using the average and the median grouping
by the given columns. We also print out the number of remaining missing
values in the feature column.
Note:
This is hard-coded for the 'LotFrontage' column.
Args:
df (pandas.DataFrame): Data frame with the pertinent data.
group_cols (list): List with the column names that we will group by
to calculate the mean and make the relvant replacements.
'''
import matplotlib.pyplot as plt
import seaborn as sns
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(12,6))
tmp = df.copy()
sns.scatterplot(y='LotFrontage', x='SalePrice', data=tmp, ax=ax1)
tmp['LotFrontage'] = tmp.groupby(group_cols)['LotFrontage'].transform(lambda x: x.fillna(x.mean()))
print('Missing values after average: {}'.format(tmp['LotFrontage'].isnull().sum()))
idxs = df['LotFrontage'].isnull()
sns.scatterplot(y='LotFrontage', x='SalePrice', data=tmp.loc[idxs], ax=ax1)
replace_price_ticks(ax1, True)
ax1.legend(labels=['Original', 'New values'])
ax1.set_title('Using average', fontsize=20)
tmp = df.copy()
sns.scatterplot(y='LotFrontage', x='SalePrice', data=tmp, ax=ax2)
tmp['LotFrontage'] = tmp.groupby(group_cols)['LotFrontage'].transform(lambda x: x.fillna(x.median()))
print('Missing values after median: {}'.format(tmp['LotFrontage'].isnull().sum()))
idxs = df['LotFrontage'].isnull()
sns.scatterplot(y='LotFrontage', x='SalePrice', data=tmp.loc[idxs], ax=ax2)
replace_price_ticks(ax2, True)
ax2.legend(labels=['Original', 'New values'])
ax2.set_title('Using median', fontsize=20)
[4]:
with open(os.path.join('_data', 'data_description.txt'), 'r') as fn:
lines = fn.readlines()
i = 0
keys = {}
contents = {}
while i < len(lines):
line = lines[i]
if ':' in line and not line.startswith(' '):
key, descrip = line.split(':')
keys[key] = descrip
if lines[i+2].startswith(' '):
i += 2
contents[key] = []
while lines[i].strip():
contents[key].append(lines[i].strip())
i += 1
if i >= len(lines): break
contents[key] = '<br>'.join(contents[key])
else:
contents[key] = 'No categories'
i += 1
Studying data#
Looking at the first few rows of the data after reading it.
[5]:
dtypes = dict(MSSubClass=str)
[6]:
df_train = pd.read_csv(os.path.join('_data', 'train.csv'), index_col=0, dtype=dtypes)
df_train.head()
[6]:
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | LotConfig | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | |||||||||||||||||||||
| 1 | 60 | RL | 65.0 | 8450 | Pave | NaN | Reg | Lvl | AllPub | Inside | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2008 | WD | Normal | 208500 |
| 2 | 20 | RL | 80.0 | 9600 | Pave | NaN | Reg | Lvl | AllPub | FR2 | ... | 0 | NaN | NaN | NaN | 0 | 5 | 2007 | WD | Normal | 181500 |
| 3 | 60 | RL | 68.0 | 11250 | Pave | NaN | IR1 | Lvl | AllPub | Inside | ... | 0 | NaN | NaN | NaN | 0 | 9 | 2008 | WD | Normal | 223500 |
| 4 | 70 | RL | 60.0 | 9550 | Pave | NaN | IR1 | Lvl | AllPub | Corner | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2006 | WD | Abnorml | 140000 |
| 5 | 60 | RL | 84.0 | 14260 | Pave | NaN | IR1 | Lvl | AllPub | FR2 | ... | 0 | NaN | NaN | NaN | 0 | 12 | 2008 | WD | Normal | 250000 |
5 rows × 80 columns
Checking for any missing values in the original data set#
[7]:
missing_vals(df_train)
[7]:
| count | percent | |
|---|---|---|
| PoolQC | 1453 | 99.520548 |
| MiscFeature | 1406 | 96.301370 |
| Alley | 1369 | 93.767123 |
| Fence | 1179 | 80.753425 |
| MasVnrType | 872 | 59.726027 |
| FireplaceQu | 690 | 47.260274 |
| LotFrontage | 259 | 17.739726 |
| GarageType | 81 | 5.547945 |
| GarageYrBlt | 81 | 5.547945 |
| GarageFinish | 81 | 5.547945 |
| GarageQual | 81 | 5.547945 |
| GarageCond | 81 | 5.547945 |
| BsmtFinType2 | 38 | 2.602740 |
| BsmtExposure | 38 | 2.602740 |
| BsmtFinType1 | 37 | 2.534247 |
| BsmtCond | 37 | 2.534247 |
| BsmtQual | 37 | 2.534247 |
| MasVnrArea | 8 | 0.547945 |
| Electrical | 1 | 0.068493 |
Making sure that there is a description for every available feature column#
The column 'SalePrice' is expected as this is the label we are trying to predict. It is not a feature in the data set.
[8]:
compare_feature_keys(keys.keys(), df_train.columns)
Keys missing in description
- Missing key SalePrice in description
Keys missing in description
Data Preprocessing#
Now that I know there are missing values in the data set 'train.csv' I will go ahead and sort out what to do with those missing values.
For the sake of brevity when I come to filling in missing data and imputing values based on other columns I will just be using the data from this single imputation. I am aware that it is often better to consider multiple imputations and to run a model for each of those methods as this can give a better performing model for unobserved data that may not fit the trends in the imputation.
[9]:
df = df_train.copy()
Outliers#
The first thing that I want to see is how normally distributed the housing price values are distributed.
[10]:
fig, ax = plt.subplots()
sns.histplot(data=df, x='SalePrice', bins=40, ax=ax)
ax.xaxis.set_minor_locator(ticker.MultipleLocator(2.5e4))
ticks = np.arange(0, 9e5, 1e5)
labels = [str(int(round(t/1e3,0))) for t in ticks]
ax.set_xticks(ticks, labels)
ax.set_xlabel('Price / 10$^3\\times$USD')
[10]:
Text(0.5, 0, 'Price / 10$^3\\times$USD')
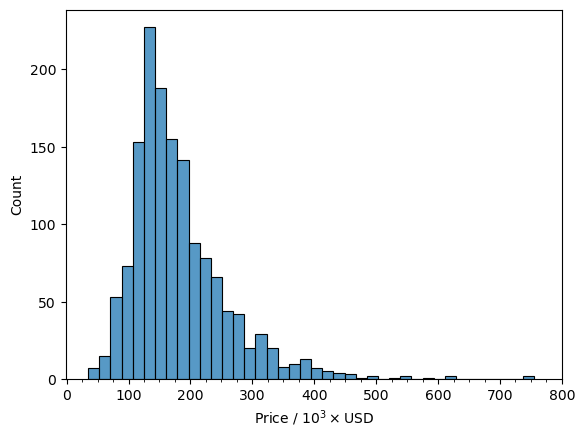
We can see that there is a very nice normal distribution of values with only a few values above 500,000 with the vast majority of values in the 120,000 to 140,000 range. I feel confident with saying that as a whole the housing prices are normally distributed as a whole. However, the houses are located in different neighborhoods so it is worthwhile to look at the prices are distributed among the different neighborhoods.
Let’s do this with a simple box plot that will also give an idea of outliers.
[11]:
fig, ax = plt.subplots(figsize=(16,6), dpi=100)
sns.boxplot(x='Neighborhood', y='SalePrice', data=df)
ax.tick_params(axis='x', labelrotation=90)
replace_price_ticks(ax, False)
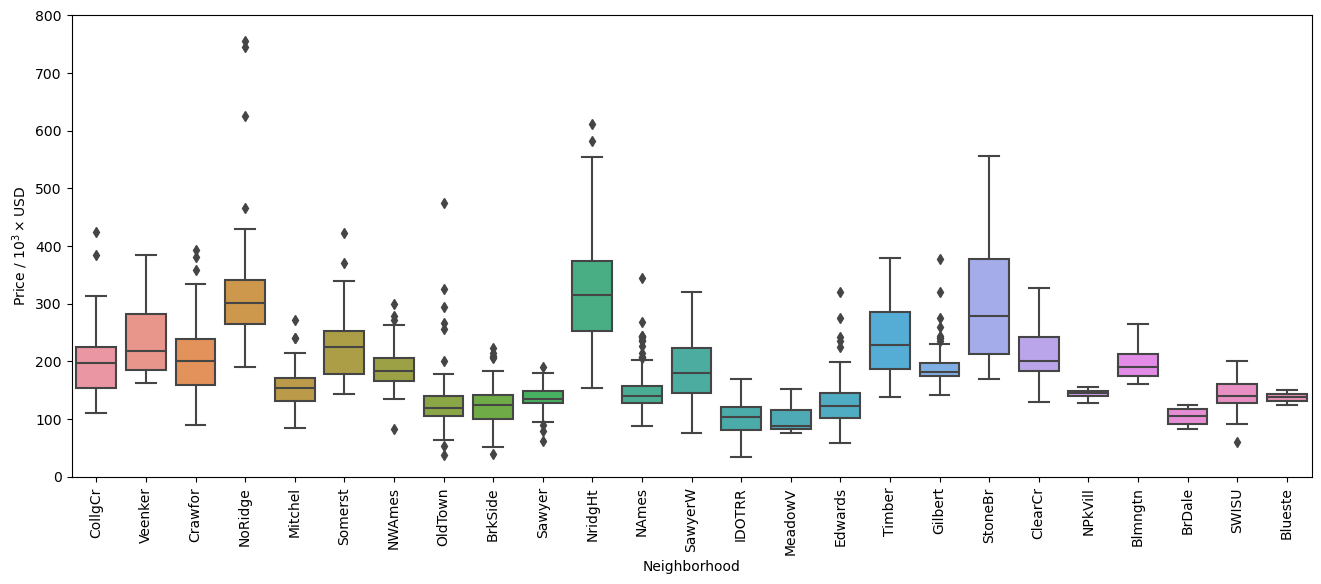
In the figure above we can see that there are many data points that are identified by Seaborn to be outside of the \(1.5 \times \text{IQR}\) (Inter-Quartile Region). Let’s look at how many are outside of this range for each neighborhood to see how much of the data falls outside this range.
[12]:
tmp = df.groupby('Neighborhood').apply(get_iqr_vals)
print("Total outside 1.5*IQR: {}".format(tmp.sum()))
tmp.sort_values(ascending=False)
Total outside 1.5*IQR: 65
[12]:
Neighborhood
NAmes 13
OldTown 8
Gilbert 8
BrkSide 6
Edwards 5
Sawyer 4
NWAmes 4
NoRidge 4
Crawfor 3
Mitchel 3
CollgCr 2
Somerst 2
NridgHt 2
SWISU 1
StoneBr 0
Timber 0
SawyerW 0
Blmngtn 0
NPkVill 0
Blueste 0
MeadowV 0
IDOTRR 0
ClearCr 0
BrDale 0
Veenker 0
dtype: int64
So there are a total of 65 values that fall outside of the \(1.5 \times \text{IQR}\), corresponding to approximately 4.5% of the data set. While these can in fact be outliers in the data set, this criteria alone is not enough to consider them outliers as they may have some useful information to the overall trends that affect the sale prices of homes. Additionally, looking at the box plots there are many points that are close to the cutoff set by Seaborn.
With this in mind it would be a good idea to find which features have a large correlation with sale prices and identify any points that break from the actual trend. This would then affect our model as it would decrease the accuracy and reliability.
Let’s start with looking at the features with the highest correlation with the sale price.
[13]:
df.corr(numeric_only=True)['SalePrice'].sort_values(key=abs, ascending=False).head(12)
[13]:
SalePrice 1.000000
OverallQual 0.790982
GrLivArea 0.708624
GarageCars 0.640409
GarageArea 0.623431
TotalBsmtSF 0.613581
1stFlrSF 0.605852
FullBath 0.560664
TotRmsAbvGrd 0.533723
YearBuilt 0.522897
YearRemodAdd 0.507101
GarageYrBlt 0.486362
Name: SalePrice, dtype: float64
We see that the feature columns 'OverallQual' and 'GrLivArea' have a correlation value over 70% and these features might be a good place to start looking for outliers.
Let’s look at the price of the house with respect to the overall quality.
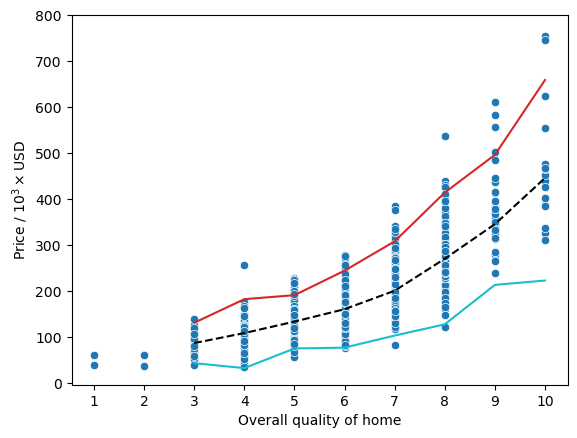
[14]:
fig, ax = plt.subplots()
sns.scatterplot(y='SalePrice', x='OverallQual', data=df, ax=ax)
iqr_high = []
iqr_low = []
median = []
x = []
for qual, data in df.groupby('OverallQual'):
if data.shape[0] < 10:
msg = "There are {} values with a quality of {}. Not plotting the IQR."
print(msg.format(data.shape[0], qual))
continue
per, iqr = calc_iqr(data['SalePrice'].values)
x.append(qual)
iqr_high.append(per[1]+1.5*iqr)
iqr_low.append(per[0]-1.5*iqr)
median.append(data['SalePrice'].median())
ax.plot(x, iqr_low, color='tab:cyan')
ax.plot(x, iqr_high, color='tab:red')
ax.plot(x, median, color='k', linestyle='--')
replace_price_ticks(ax, False)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.set_xlabel('Overall quality of home')
There are 2 values with a quality of 1. Not plotting the IQR.
There are 3 values with a quality of 2. Not plotting the IQR.
[14]:
Text(0.5, 0, 'Overall quality of home')
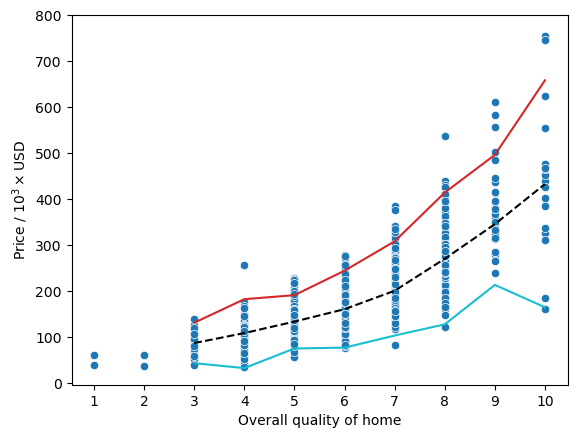
Here, we can actually see a pretty good relationship between the price of a home and the overall quality as denoted by the black dashed line representing the median for each quality rating. However, we can also see that there are a couple houses that have an overall quality rating of 10 and a price less than 200,000 where the cyan line representing \(1.5 \times \text{IQR}\) subtracted from the 25th percentile has a small dip in the trend.
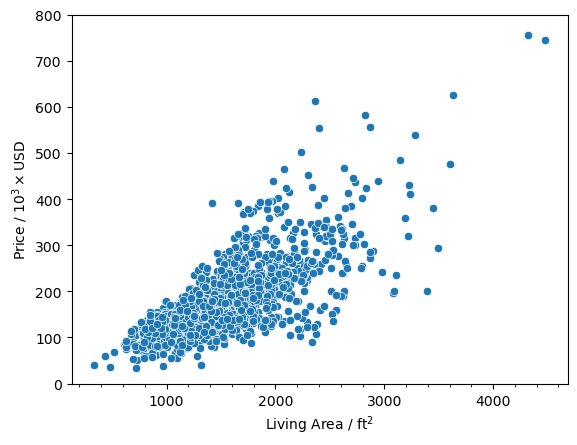
Before we jump to conclusions let’s look at another plot with the 'GrLivArea' which is the above ground living area.
[15]:
fig, ax = plt.subplots()
sns.scatterplot(y='SalePrice', x='GrLivArea', data=df, ax=ax)
replace_price_ticks(ax, False)
ax.xaxis.set_minor_locator(ticker.MultipleLocator(200))
ax.set_xlabel('Living Area / ft$^2$')
[15]:
Text(0.5, 0, 'Living Area / ft$^2$')
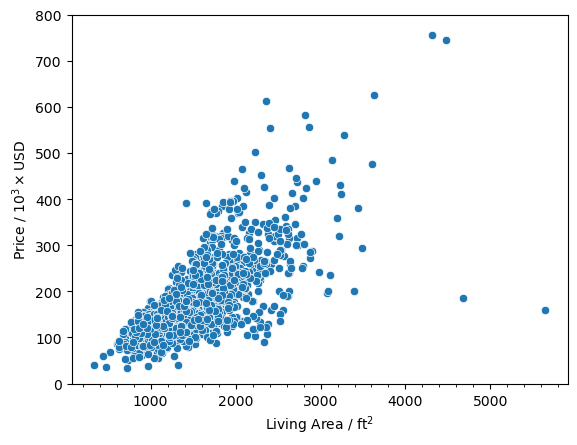
And we see that there are two points that have a square footage greater than 4000 and a price less than 200,000. Now let’s look at the data points and see if they are the same.
[16]:
df.loc[(df['OverallQual'] == 10) & (df['SalePrice'] < 200e3)]
[16]:
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | LotConfig | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | |||||||||||||||||||||
| 524 | 60 | RL | 130.0 | 40094 | Pave | NaN | IR1 | Bnk | AllPub | Inside | ... | 0 | NaN | NaN | NaN | 0 | 10 | 2007 | New | Partial | 184750 |
| 1299 | 60 | RL | 313.0 | 63887 | Pave | NaN | IR3 | Bnk | AllPub | Corner | ... | 480 | Gd | NaN | NaN | 0 | 1 | 2008 | New | Partial | 160000 |
2 rows × 80 columns
[17]:
df.loc[(df['GrLivArea'] > 4000) & (df['SalePrice'] < 200e3)]
[17]:
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | LotConfig | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | |||||||||||||||||||||
| 524 | 60 | RL | 130.0 | 40094 | Pave | NaN | IR1 | Bnk | AllPub | Inside | ... | 0 | NaN | NaN | NaN | 0 | 10 | 2007 | New | Partial | 184750 |
| 1299 | 60 | RL | 313.0 | 63887 | Pave | NaN | IR3 | Bnk | AllPub | Corner | ... | 480 | Gd | NaN | NaN | 0 | 1 | 2008 | New | Partial | 160000 |
2 rows × 80 columns
And we can see that they are the same data points. I am labeling these as outlier points since they don’t fall nicely within the overall trend that we can see for 'OverallQual' and 'GrLivArea'. The values that we initially found to be above 500,000 are not outliers because they actually fall within the trends. They are just on the expensive end of the spectrum so they may give us valuable information for the model.
[18]:
idxs = df.loc[(df['OverallQual'] == 10) & (df['SalePrice'] < 200e3)].index
df.drop(idxs, axis=0, inplace=True)
[19]:
fig, ax = plt.subplots()
sns.scatterplot(y='SalePrice', x='OverallQual', data=df, ax=ax)
iqr_high = []
iqr_low = []
median = []
x = []
for qual, data in df.groupby('OverallQual'):
if data.shape[0] < 10:
msg = "There are {} values with a quality of {}. Not plotting the IQR."
print(msg.format(data.shape[0], qual))
continue
per, iqr = calc_iqr(data['SalePrice'].values)
x.append(qual)
iqr_high.append(per[1]+1.5*iqr)
iqr_low.append(per[0]-1.5*iqr)
median.append(data['SalePrice'].median())
ax.plot(x, iqr_low, color='tab:cyan')
ax.plot(x, iqr_high, color='tab:red')
ax.plot(x, median, color='k', linestyle='--')
replace_price_ticks(ax, False)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.set_xlabel('Overall quality of home')
There are 2 values with a quality of 1. Not plotting the IQR.
There are 3 values with a quality of 2. Not plotting the IQR.
[19]:
Text(0.5, 0, 'Overall quality of home')
[20]:
fig, ax = plt.subplots()
sns.scatterplot(y='SalePrice', x='GrLivArea', data=df, ax=ax)
replace_price_ticks(ax, False)
ax.xaxis.set_minor_locator(ticker.MultipleLocator(200))
ax.set_xlabel('Living Area / ft$^2$')
[20]:
Text(0.5, 0, 'Living Area / ft$^2$')
[21]:
df.corr(numeric_only=True)['SalePrice'].sort_values(key=abs, ascending=False).head(8)
[21]:
SalePrice 1.000000
OverallQual 0.795774
GrLivArea 0.734968
TotalBsmtSF 0.651153
GarageCars 0.641047
1stFlrSF 0.631530
GarageArea 0.629217
FullBath 0.562165
Name: SalePrice, dtype: float64
Now we have a nicely defined linear trend for the sale price with respect to the living area. We can also see that the correlation values went up slightly for 'OverallQual' and 'GrLivArea'.
Electrical#
First thing I want to determine is if there are any rows that I can simply drop because getting the values for the missing data might just not make too much sense and I can simply drop the data point altogether.
So let’s look at the number of missing values again.
[22]:
missing_vals(df)
[22]:
| count | percent | |
|---|---|---|
| PoolQC | 1452 | 99.588477 |
| MiscFeature | 1404 | 96.296296 |
| Alley | 1367 | 93.758573 |
| Fence | 1177 | 80.727023 |
| MasVnrType | 872 | 59.807956 |
| FireplaceQu | 690 | 47.325103 |
| LotFrontage | 259 | 17.764060 |
| GarageType | 81 | 5.555556 |
| GarageYrBlt | 81 | 5.555556 |
| GarageFinish | 81 | 5.555556 |
| GarageQual | 81 | 5.555556 |
| GarageCond | 81 | 5.555556 |
| BsmtFinType2 | 38 | 2.606310 |
| BsmtExposure | 38 | 2.606310 |
| BsmtFinType1 | 37 | 2.537723 |
| BsmtCond | 37 | 2.537723 |
| BsmtQual | 37 | 2.537723 |
| MasVnrArea | 8 | 0.548697 |
| Electrical | 1 | 0.068587 |
The more curious one to study is the feature column 'Electrical' as there is only one missing value that accounts for 0.07% of the availble data. Before I just drop the row I want to look at the description of it which is
Electrical: Electrical system
SBrkr Standard Circuit Breakers & Romex
FuseA Fuse Box over 60 AMP and all Romex wiring (Average)
FuseF 60 AMP Fuse Box and mostly Romex wiring (Fair)
FuseP 60 AMP Fuse Box and mostly knob & tube wiring (poor)
Mix Mixed
Typically, since there is only one row that is missing data it can be safe enough to just drop that row entirely as it only accounts for 0.07% of the data set. However, I want to try to infer the value based on some metric.
First let’s look at some of the columns associated with the row that is missing data. I have identified the dwelling type ('MSSubClass'), zoning type ('MSZoning'), and neighborhood ('Neighborhood') as potential columns that may be important in determining what kind of electrical system the building should have.
[23]:
df.loc[df['Electrical'].isnull(), ['Electrical', 'MSSubClass', 'MSZoning', 'Neighborhood', 'SalePrice']]
[23]:
| Electrical | MSSubClass | MSZoning | Neighborhood | SalePrice | |
|---|---|---|---|---|---|
| Id | |||||
| 1380 | NaN | 80 | RL | Timber | 167500 |
Before we do anything let’s look at some of the statistics from the sale price ('SalePrice') with the type of electrical system.
[24]:
df.groupby('Electrical')['SalePrice'].describe().sort_values(by=['mean'], ascending=False)
[24]:
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| Electrical | ||||||||
| SBrkr | 1332.0 | 186846.810060 | 79913.027373 | 37900.0 | 134500.0 | 170000.0 | 221000.00 | 755000.0 |
| FuseA | 94.0 | 122196.893617 | 37511.376615 | 34900.0 | 98500.0 | 121250.0 | 143531.25 | 239000.0 |
| FuseF | 27.0 | 107675.444444 | 30636.507376 | 39300.0 | 88500.0 | 115000.0 | 129950.00 | 169500.0 |
| FuseP | 3.0 | 97333.333333 | 34645.827070 | 73000.0 | 77500.0 | 82000.0 | 109500.00 | 137000.0 |
| Mix | 1.0 | 67000.000000 | NaN | 67000.0 | 67000.0 | 67000.0 | 67000.00 | 67000.0 |
We can see that the average price is actually the highest with the standard circuit breakers and romex ('SBrkr'). However, you can also see that and electrical system 'SBrkr' is actually in over 90% of the homes so it’s hard to make any conclusions on the effect of the electrical system on the final sale price.
Now let’s try to take a look at the distributions in the other categorical values.
We start with a Box Plot of the sale prices against the electrical system used.
[25]:
sns.boxplot(x='SalePrice', y='Electrical', data=df,
order=['SBrkr', 'FuseA', 'FuseF', 'FuseP', 'Mix'])
[25]:
<Axes: xlabel='SalePrice', ylabel='Electrical'>
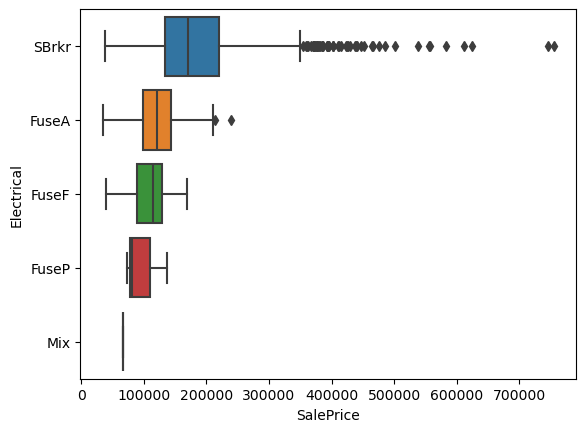
Since this is just a pictorial representation of the statistical data, the overall conclusions are the same. However, we can see that the median of the data for 'SBrkr' is in the lower range of the distribution and there are a lot of points outside of the \(1.5 \times \text{IQR}\) range as defined in Seaborn. While this can, in some cases, be identified as outliers, this is clearly not that case as the points are continuous.
Next we have a set of pictorial representations of the Pandas pivot table to look at the total number of electrical systems in each of the categorical classifications. At the end we will break down each of the plots and try to connect them with our data.
We start with the type dwelling.
[67]:
gen_cat_matrix(df=df, x='MSSubClass', y='Electrical')
[67]:
| Electrical | FuseA | FuseF | FuseP | Mix | SBrkr |
|---|---|---|---|---|---|
| MSSubClass | |||||
| 120 | 0 | 0 | 0 | 0 | 87 |
| 160 | 0 | 0 | 0 | 0 | 63 |
| 180 | 0 | 0 | 0 | 0 | 10 |
| 190 | 5 | 1 | 1 | 0 | 23 |
| 20 | 31 | 5 | 0 | 0 | 500 |
| 30 | 18 | 4 | 1 | 1 | 45 |
| 40 | 2 | 0 | 0 | 0 | 2 |
| 45 | 3 | 2 | 0 | 0 | 7 |
| 50 | 20 | 8 | 0 | 0 | 116 |
| 60 | 0 | 0 | 0 | 0 | 297 |
| 70 | 8 | 2 | 0 | 0 | 50 |
| 75 | 2 | 0 | 0 | 0 | 14 |
| 80 | 0 | 1 | 0 | 0 | 56 |
| 85 | 0 | 0 | 0 | 0 | 20 |
| 90 | 5 | 4 | 1 | 0 | 42 |
Next is the zoning type.
[68]:
gen_cat_matrix(df=df, x='MSZoning', y='Electrical')
[68]:
| Electrical | FuseA | FuseF | FuseP | Mix | SBrkr |
|---|---|---|---|---|---|
| MSZoning | |||||
| C (all) | 4 | 0 | 0 | 0 | 6 |
| FV | 0 | 0 | 0 | 0 | 65 |
| RH | 4 | 1 | 0 | 0 | 11 |
| RL | 56 | 18 | 1 | 0 | 1073 |
| RM | 30 | 8 | 2 | 1 | 177 |
The neighborhood the dwelling is located in.
[69]:
gen_cat_matrix(df=df, x='Neighborhood', y='Electrical', linewidth=0.5)
[69]:
| Electrical | FuseA | FuseF | FuseP | Mix | SBrkr |
|---|---|---|---|---|---|
| Neighborhood | |||||
| Blmngtn | 0 | 0 | 0 | 0 | 17 |
| Blueste | 0 | 0 | 0 | 0 | 2 |
| BrDale | 0 | 0 | 0 | 0 | 16 |
| BrkSide | 13 | 3 | 0 | 0 | 42 |
| ClearCr | 2 | 1 | 0 | 0 | 25 |
| CollgCr | 0 | 0 | 0 | 0 | 150 |
| Crawfor | 3 | 2 | 0 | 0 | 46 |
| Edwards | 12 | 9 | 1 | 0 | 76 |
| Gilbert | 0 | 0 | 0 | 0 | 79 |
| IDOTRR | 10 | 4 | 0 | 1 | 22 |
| MeadowV | 0 | 0 | 0 | 0 | 17 |
| Mitchel | 1 | 0 | 0 | 0 | 48 |
| NAmes | 27 | 3 | 0 | 0 | 195 |
| NPkVill | 0 | 0 | 0 | 0 | 9 |
| NWAmes | 0 | 0 | 0 | 0 | 73 |
| NoRidge | 0 | 0 | 0 | 0 | 41 |
| NridgHt | 0 | 0 | 0 | 0 | 77 |
| OldTown | 21 | 3 | 2 | 0 | 87 |
| SWISU | 3 | 2 | 0 | 0 | 20 |
| Sawyer | 0 | 0 | 0 | 0 | 74 |
| SawyerW | 1 | 0 | 0 | 0 | 58 |
| Somerst | 0 | 0 | 0 | 0 | 86 |
| StoneBr | 0 | 0 | 0 | 0 | 25 |
| Timber | 1 | 0 | 0 | 0 | 36 |
| Veenker | 0 | 0 | 0 | 0 | 11 |
Based on the plots above I can see that there is no real connection between what type of electrical system a building has and its location, dwelling type, or zoning type. They pretty much all have a standard breaker system, 'SBrkr'. With this in mind I believe that it is safe to perfrom a replacement of the missing value with the mode for the neighborhood the home is located.
The next two are trying to identify any relationship between the zoning type and the type of dwelling and neighborhood, respectively. I do not believe that this will give any extra valuable information, however, the North Ames neighborhood, 'NAmes', has the highest number of homes that use an electrcial system classified as 'FuseA'. If there were more data points missing, it would be interesting to see if it would be necessary to consider some kind of distribution to try to retain the
original ratios the same.
[70]:
gen_cat_matrix(df=df, x='MSSubClass', y='MSZoning')
[70]:
| MSZoning | C (all) | FV | RH | RL | RM |
|---|---|---|---|---|---|
| MSSubClass | |||||
| 120 | 0 | 5 | 2 | 59 | 21 |
| 160 | 0 | 22 | 0 | 11 | 30 |
| 180 | 0 | 0 | 0 | 0 | 10 |
| 190 | 1 | 0 | 2 | 16 | 11 |
| 20 | 2 | 13 | 3 | 508 | 10 |
| 30 | 2 | 0 | 1 | 33 | 33 |
| 40 | 0 | 0 | 0 | 2 | 2 |
| 45 | 0 | 0 | 1 | 4 | 7 |
| 50 | 4 | 0 | 1 | 88 | 51 |
| 60 | 0 | 25 | 0 | 271 | 1 |
| 70 | 1 | 0 | 3 | 30 | 26 |
| 75 | 0 | 0 | 0 | 6 | 10 |
| 80 | 0 | 0 | 0 | 58 | 0 |
| 85 | 0 | 0 | 0 | 20 | 0 |
| 90 | 0 | 0 | 3 | 43 | 6 |
[71]:
gen_cat_matrix(df=df, x='Neighborhood', y='MSZoning', linewidth=0.5)
[71]:
| MSZoning | C (all) | FV | RH | RL | RM |
|---|---|---|---|---|---|
| Neighborhood | |||||
| Blmngtn | 0 | 0 | 0 | 16 | 1 |
| Blueste | 0 | 0 | 0 | 0 | 2 |
| BrDale | 0 | 0 | 0 | 0 | 16 |
| BrkSide | 0 | 0 | 0 | 28 | 30 |
| ClearCr | 0 | 0 | 0 | 28 | 0 |
| CollgCr | 0 | 0 | 0 | 140 | 10 |
| Crawfor | 0 | 0 | 2 | 46 | 3 |
| Edwards | 0 | 0 | 2 | 88 | 8 |
| Gilbert | 0 | 0 | 0 | 79 | 0 |
| IDOTRR | 9 | 0 | 0 | 0 | 28 |
| MeadowV | 0 | 0 | 0 | 0 | 17 |
| Mitchel | 0 | 0 | 0 | 44 | 5 |
| NAmes | 0 | 0 | 2 | 223 | 0 |
| NPkVill | 0 | 0 | 0 | 9 | 0 |
| NWAmes | 0 | 0 | 0 | 73 | 0 |
| NoRidge | 0 | 0 | 0 | 41 | 0 |
| NridgHt | 0 | 0 | 0 | 76 | 1 |
| OldTown | 1 | 0 | 0 | 17 | 95 |
| SWISU | 0 | 0 | 5 | 20 | 0 |
| Sawyer | 0 | 0 | 0 | 72 | 2 |
| SawyerW | 0 | 0 | 5 | 54 | 0 |
| Somerst | 0 | 65 | 0 | 21 | 0 |
| StoneBr | 0 | 0 | 0 | 25 | 0 |
| Timber | 0 | 0 | 0 | 38 | 0 |
| Veenker | 0 | 0 | 0 | 11 | 0 |
So as mentioned before there is no extra information that we will gather from the two plots above.
Now let’s make the replacement with the overall mode of the neighborhood the missing value is in.
[30]:
group_cols = ['Neighborhood', 'MSSubClass', 'MSZoning']
df['Electrical'] = df.groupby(group_cols)['Electrical'].transform(fill_mode)
[31]:
missing_vals(df)
[31]:
| count | percent | |
|---|---|---|
| PoolQC | 1452 | 99.588477 |
| MiscFeature | 1404 | 96.296296 |
| Alley | 1367 | 93.758573 |
| Fence | 1177 | 80.727023 |
| MasVnrType | 872 | 59.807956 |
| FireplaceQu | 690 | 47.325103 |
| LotFrontage | 259 | 17.764060 |
| GarageType | 81 | 5.555556 |
| GarageYrBlt | 81 | 5.555556 |
| GarageFinish | 81 | 5.555556 |
| GarageQual | 81 | 5.555556 |
| GarageCond | 81 | 5.555556 |
| BsmtExposure | 38 | 2.606310 |
| BsmtFinType2 | 38 | 2.606310 |
| BsmtFinType1 | 37 | 2.537723 |
| BsmtCond | 37 | 2.537723 |
| BsmtQual | 37 | 2.537723 |
| MasVnrArea | 8 | 0.548697 |
And we have gotten rid of the missing value.
In reality, it might actually be good enough to just drop that row altogether since it is one row accounting for 0.07% of the data set. However, if there are more values missing, ~40 rows or 2.7%, just dropping the rows might not be the best thing to do. Especially if we end up doing this for multiple columns that may not share the same indeces. It can really add up in the end.
Masonry Veneer#
From the previous cell we can see that we are missing values in the 'MasVnrArea' and 'MasVnrType' columns. Below is a description of the columns.
MasVnrType: Masonry veneer type
BrkCmn Brick Common
BrkFace Brick Face
CBlock Cinder Block
None None
Stone Stone
MasVnrArea: Masonry veneer area in square feet
So we can see that it has to do with the masonry veneer that the house has. More importantly, we can see that for the 'MasVnrType', when there is a missing value it just means that there is no masonry veneer. This can be further supported by the 'MasVnrArea', which is the area covered by the masonry veneer and should be zero if the 'MasVnrType' is missing a value. However, we must be careful as the 'MasVnrArea' feature is missing some data points. As this is a numerical value it
might be hard to determine what it should be. I will go into this one in more detail later on.
So let’s first take where the values of 'MasVnrType' is missing a value and see what are the values of 'MasVnrArea'.
[32]:
df.loc[df['MasVnrType'].isnull(), ['MasVnrType', 'MasVnrArea']].value_counts(dropna=False)
[32]:
MasVnrType MasVnrArea
NaN 0.0 859
NaN 8
1.0 2
288.0 1
312.0 1
344.0 1
Name: count, dtype: int64
What we see is that there are a lot of places where the 'MasVnrType' is missing a value and 'MasVnrArea' is 0.0. However, when we were looking at the percentges of missing values above we could see that the 'MasVnrArea' feature was missing values as well and we can see that here.
Therefore, we have to be careful in how we perform the replacement as we must replace the NaN values in 'MasVnrType' for 'None' only where 'MasVnrArea' is 0.0.
[33]:
df.loc[(df['MasVnrType'].isnull()) & (df['MasVnrArea'] == 0.0), ['MasVnrType']] = 'None'
Now let’s try to determine what we should do with the other values in these columns.
[34]:
df.loc[df['MasVnrType'].isnull(), ['MasVnrType', 'MasVnrArea']].value_counts(dropna=False)
[34]:
MasVnrType MasVnrArea
NaN NaN 8
1.0 2
288.0 1
312.0 1
344.0 1
Name: count, dtype: int64
Now we are just missing values when 'MasVnrArea' is either NaN or non-zero.
Let’s look into the distribution of the values with respect to the sale price. What I want to determine is how correlated are the values and will some simple replacements create outliers in our data set.
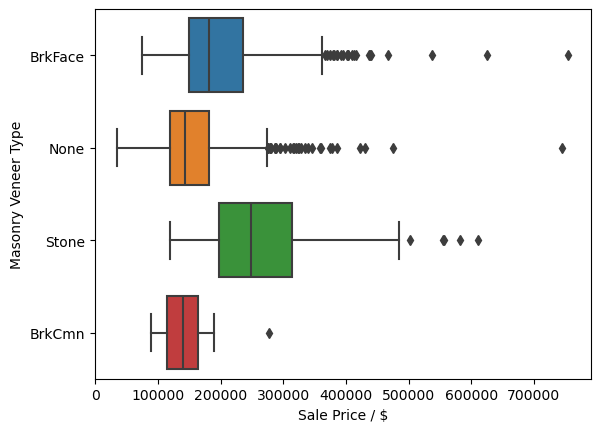
[35]:
sns.boxplot(x='SalePrice', y='MasVnrType', data=df)
plt.ylabel('Masonry Veneer Type')
plt.xlabel('Sale Price / $')
[35]:
Text(0.5, 0, 'Sale Price / $')
[36]:
sns.scatterplot(x='SalePrice', y='MasVnrArea', data=df)
plt.ylabel('Masonry Veneer Area / ft$^2$')
plt.xlabel('Sale Price / $')
[36]:
Text(0.5, 0, 'Sale Price / $')
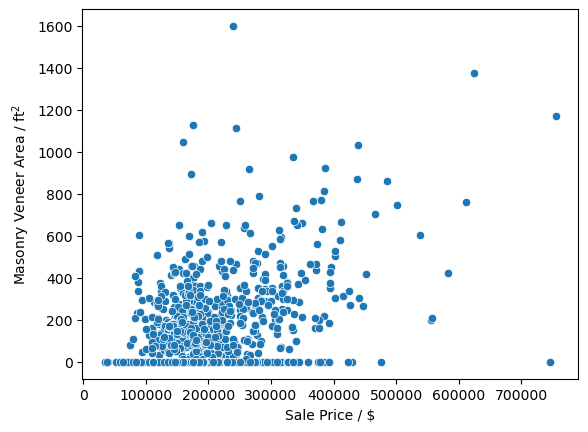
There does not seem to ba a very large correlation between the type of masonry veneer or its type on the sale price of a home. Due to this I will go ahead and replace all NaN values with 0.0 and 'None' in the 'MasVnrArea' and 'MasVnrType', respectively. Since there is no large correlation between the values and the sale price I feel confident in also making the replacement of all the values of 'MasVnrType' with 'None', even when the 'MasVnrArea' is not zero.
[37]:
df['MasVnrArea'] = df['MasVnrArea'].fillna(0.0)
df['MasVnrType'] = df['MasVnrType'].fillna('None')
[38]:
missing_vals(df)
[38]:
| count | percent | |
|---|---|---|
| PoolQC | 1452 | 99.588477 |
| MiscFeature | 1404 | 96.296296 |
| Alley | 1367 | 93.758573 |
| Fence | 1177 | 80.727023 |
| FireplaceQu | 690 | 47.325103 |
| LotFrontage | 259 | 17.764060 |
| GarageType | 81 | 5.555556 |
| GarageYrBlt | 81 | 5.555556 |
| GarageFinish | 81 | 5.555556 |
| GarageQual | 81 | 5.555556 |
| GarageCond | 81 | 5.555556 |
| BsmtExposure | 38 | 2.606310 |
| BsmtFinType2 | 38 | 2.606310 |
| BsmtQual | 37 | 2.537723 |
| BsmtCond | 37 | 2.537723 |
| BsmtFinType1 | 37 | 2.537723 |
And now we have no missing values for the 'MasVnrType' when the 'MasVnrArea' is zero.
Basement#
The next values that I want to tackle are going to be concerned with the basement data. The description for all the available feature columns for basements are
BsmtQual: Evaluates the height of the basement
Ex Excellent (100+ inches)
Gd Good (90-99 inches)
TA Typical (80-89 inches)
Fa Fair (70-79 inches)
Po Poor (<70 inches
NA No Basement
BsmtCond: Evaluates the general condition of the basement
Ex Excellent
Gd Good
TA Typical - slight dampness allowed
Fa Fair - dampness or some cracking or settling
Po Poor - Severe cracking, settling, or wetness
NA No Basement
BsmtExposure: Refers to walkout or garden level walls
Gd Good Exposure
Av Average Exposure (split levels or foyers typically score average or above)
Mn Mimimum Exposure
No No Exposure
NA No Basement
BsmtFinType1: Rating of basement finished area
GLQ Good Living Quarters
ALQ Average Living Quarters
BLQ Below Average Living Quarters
Rec Average Rec Room
LwQ Low Quality
Unf Unfinshed
NA No Basement
BsmtFinSF1: Type 1 finished square feet
BsmtFinType2: Rating of basement finished area (if multiple types)
GLQ Good Living Quarters
ALQ Average Living Quarters
BLQ Below Average Living Quarters
Rec Average Rec Room
LwQ Low Quality
Unf Unfinshed
NA No Basement
BsmtFinSF2: Type 2 finished square feet
BsmtUnfSF: Unfinished square feet of basement area
TotalBsmtSF: Total square feet of basement area
So, similar to before we can see that a lot of the data that is missing for the basements is categorical and we can probably fill in a lot of the NaN values with 'None' as there is probably no basement there.
Let’s confirm this below by getting the square footage and other things like we did for the 'MasVnrType' feature.
[39]:
df.loc[df['BsmtCond'].isnull(), [x for x in df.columns if 'bsmt' in x.lower()]].value_counts(dropna=False)
[39]:
BsmtQual BsmtCond BsmtExposure BsmtFinType1 BsmtFinSF1 BsmtFinType2 BsmtFinSF2 BsmtUnfSF TotalBsmtSF BsmtFullBath BsmtHalfBath
NaN NaN NaN NaN 0 NaN 0 0 0 0 0 37
Name: count, dtype: int64
And we can see that for all the categorical values, if the numerical features, 'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF', and 'TotalBsmtSF', it is missing a value, supporting our initial guess. However, looking at the data frame for the missing values
[40]:
missing_vals(df).loc[['BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2']]
[40]:
| count | percent | |
|---|---|---|
| BsmtQual | 37 | 2.537723 |
| BsmtCond | 37 | 2.537723 |
| BsmtExposure | 38 | 2.606310 |
| BsmtFinType1 | 37 | 2.537723 |
| BsmtFinType2 | 38 | 2.606310 |
Let’s go ahead and replace the categorical values for all the columns when 'BsmtCond' is NaN with 'None'.
[41]:
cat_cols = ['BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2']
df.loc[df['BsmtCond'].isnull(), cat_cols] = 'None'
Let’s check for missing values.
[42]:
missing_vals(df)
[42]:
| count | percent | |
|---|---|---|
| PoolQC | 1452 | 99.588477 |
| MiscFeature | 1404 | 96.296296 |
| Alley | 1367 | 93.758573 |
| Fence | 1177 | 80.727023 |
| FireplaceQu | 690 | 47.325103 |
| LotFrontage | 259 | 17.764060 |
| GarageType | 81 | 5.555556 |
| GarageYrBlt | 81 | 5.555556 |
| GarageFinish | 81 | 5.555556 |
| GarageQual | 81 | 5.555556 |
| GarageCond | 81 | 5.555556 |
| BsmtExposure | 1 | 0.068587 |
| BsmtFinType2 | 1 | 0.068587 |
And we still have values missing for the 'BsmtExposure' and 'BsmtFinType2' columns.
Below is the data for when the other two columns are missing data.
[43]:
df.loc[(df['BsmtFinType2'].isnull()) & (~df['BsmtCond'].isnull()), [x for x in df.columns if 'bsmt' in x.lower()]]
[43]:
| BsmtQual | BsmtCond | BsmtExposure | BsmtFinType1 | BsmtFinSF1 | BsmtFinType2 | BsmtFinSF2 | BsmtUnfSF | TotalBsmtSF | BsmtFullBath | BsmtHalfBath | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | |||||||||||
| 333 | Gd | TA | No | GLQ | 1124 | NaN | 479 | 1603 | 3206 | 1 | 0 |
[44]:
df.loc[(df['BsmtExposure'].isnull()) & (~df['BsmtCond'].isnull()), [x for x in df.columns if 'bsmt' in x.lower()]]
[44]:
| BsmtQual | BsmtCond | BsmtExposure | BsmtFinType1 | BsmtFinSF1 | BsmtFinType2 | BsmtFinSF2 | BsmtUnfSF | TotalBsmtSF | BsmtFullBath | BsmtHalfBath | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | |||||||||||
| 949 | Gd | TA | NaN | Unf | 0 | Unf | 0 | 936 | 936 | 0 | 0 |
Well, we can actually see that 'BsmtFinType2' and 'BsmtExposure' do not share missing values on the same row and this data should not actually be missing. Data for 'BsmtFinType2' should only be missing when 'BsmtFinType2' is 0 and 'BsmtExposure' should only be missing when there is no basement, i.e. when 'TotalBsmtSF' is 0. This is somewhat problematic and will require looking at a few other things before deciding on what should be done.
So let’s take a look at how dependent the sale price, 'SalePrice', is to the different categorical values for the basement in our data set. The y-axis will be labeled from worst (bottom) to best (top) in terms of quality or the metric used for the categorical labels.
[45]:
fig, ax = plt.subplots(figsize=(12, 12), nrows=3, ncols=2)
ax = ax.flatten()
cols = ['BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2']
labels = ['Quality', 'Condition', 'Exposure', 'Finish', 'Finish (if multiple)']
orders = dict(BsmtQual=['Ex', 'Gd', 'TA', 'Fa', 'Po'],
BsmtCond=['Ex', 'Gd', 'TA', 'Fa', 'Po'],
BsmtExposure=['Gd', 'Av', 'Mn', 'No'],
BsmtFinType1=['GLQ', 'ALQ', 'BLQ', 'Rec', 'LwQ', 'Unf'],
BsmtFinType2=['GLQ', 'ALQ', 'BLQ', 'Rec', 'LwQ', 'Unf'])
for i, (col, label) in enumerate(zip(cols, labels)):
sns.boxplot(x='SalePrice', y=col, data=df, ax=ax[i],
order=orders[col])
ax[i].xaxis.set_minor_locator(ticker.MultipleLocator(2.5e4))
ticks = np.arange(0, 9e5, 1e5)
labels = [str(int(round(t/1e3,0))) for t in ticks]
ax[i].set_xticks(ticks, labels)
ax[i].set_xlabel('Price / 10$^3\\times$USD')
ax[i].set_ylabel(label+f' ({col})')
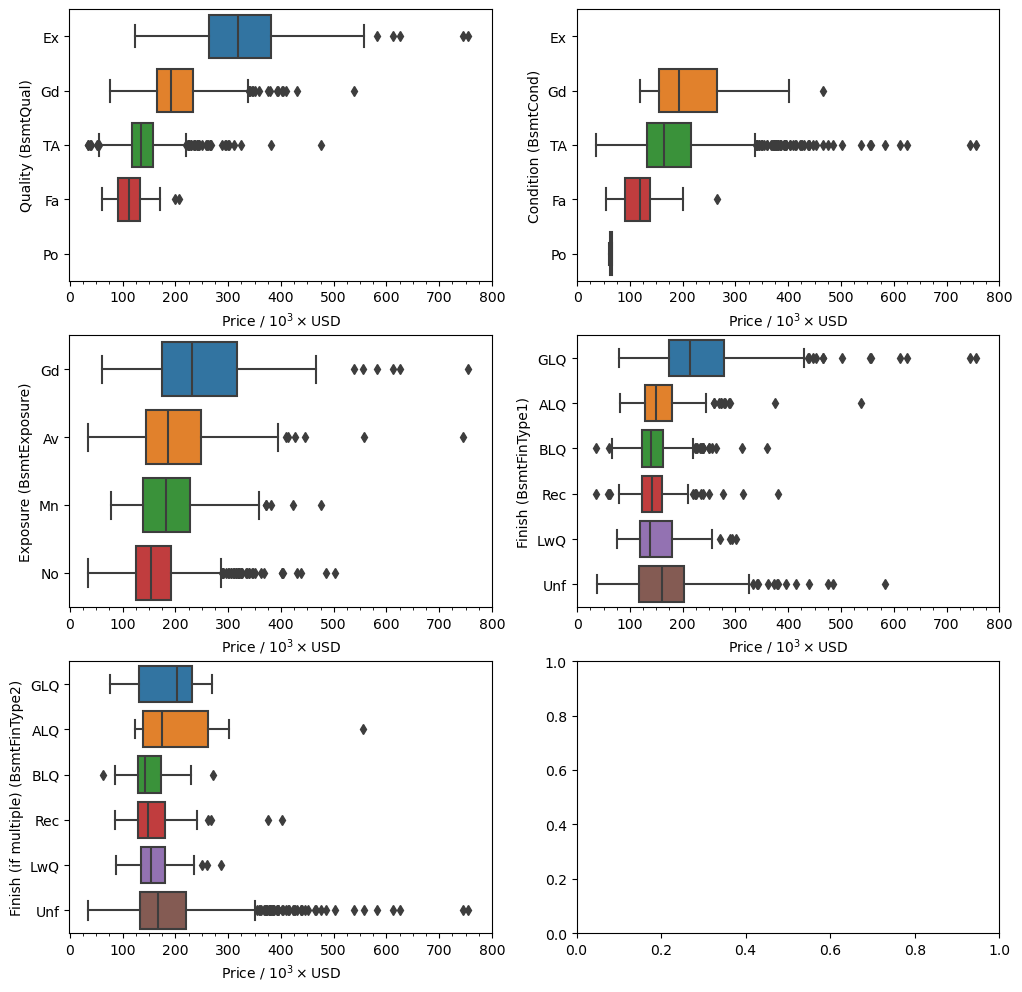
What we can see here is that there is a stronger correlation between the sale price of a house and the basement quality ('BsmtQual') and condition ('BsmtCond') than with the other categorical features. From before we are missing values in the 'BsmtExposure' and 'BsmtFinType2' features, but we have already seen that they should not be missing. Based on what I see on the plots above I believe it is safe to replace the missing values for the two rows with an imputed value based on
the mode of the column with respect to the neighborhood the house is in and the type of dwelling. Before we do so let’s make sure that this will actually make sense.
Here’s the data for the row missing the 'BsmtExposure' value.
[46]:
df.loc[(df['BsmtExposure'].isnull()) & (~df['BsmtCond'].isnull()),
[x for x in df.columns if 'bsmt' in x.lower()]+['Neighborhood', 'MSSubClass']].T
[46]:
| Id | 949 |
|---|---|
| BsmtQual | Gd |
| BsmtCond | TA |
| BsmtExposure | NaN |
| BsmtFinType1 | Unf |
| BsmtFinSF1 | 0 |
| BsmtFinType2 | Unf |
| BsmtFinSF2 | 0 |
| BsmtUnfSF | 936 |
| TotalBsmtSF | 936 |
| BsmtFullBath | 0 |
| BsmtHalfBath | 0 |
| Neighborhood | CollgCr |
| MSSubClass | 60 |
A breakdown of the basement exposure for each dwelling type in the College Creek ('CollgCr') neighborhood.
[47]:
df.groupby(['Neighborhood', 'MSSubClass'])['BsmtExposure'].value_counts(dropna=False).loc['CollgCr']
[47]:
MSSubClass BsmtExposure
120 Av 7
Gd 2
Mn 1
20 Av 35
No 32
Gd 8
Mn 6
60 No 33
Av 11
Mn 7
NaN 1
Gd 1
80 Av 2
Gd 1
85 Av 3
Name: count, dtype: int64
We know that our missing row has the label '60' for the dwelling type and we see that the mode is that there is no exposure. I believe this is a fair enough assumption given that this is a 2 story home. So let’s make the replacement in a generalized fashion with the transform method in pandas.
Some of the potential pitfalls of this type of replacement is that if the mode of the data is actually ``NaN`` then you may end up just replacing a ``NaN`` value with another ``NaN`` value.
[48]:
df['BsmtExposure'] = df.groupby(['Neighborhood', 'MSSubClass'])['BsmtExposure'].transform(fill_mode)
And now let’s look at the other problematic column, 'BsmtFinType2'.
Here is the data in the missing row.
[49]:
df.loc[(df['BsmtFinType2'].isnull()) & (~df['BsmtCond'].isnull()),
[x for x in df.columns if 'bsmt' in x.lower()]+['Neighborhood', 'MSSubClass']].T
[49]:
| Id | 333 |
|---|---|
| BsmtQual | Gd |
| BsmtCond | TA |
| BsmtExposure | No |
| BsmtFinType1 | GLQ |
| BsmtFinSF1 | 1124 |
| BsmtFinType2 | NaN |
| BsmtFinSF2 | 479 |
| BsmtUnfSF | 1603 |
| TotalBsmtSF | 3206 |
| BsmtFullBath | 1 |
| BsmtHalfBath | 0 |
| Neighborhood | NridgHt |
| MSSubClass | 20 |
[50]:
df.groupby(['Neighborhood', 'MSSubClass'])['BsmtFinType2'].value_counts(dropna=False).loc['NridgHt']
[50]:
MSSubClass BsmtFinType2
120 Unf 19
160 Unf 3
20 Unf 30
ALQ 1
NaN 1
60 Unf 23
Name: count, dtype: int64
So most of the houses actually don’t have a second type of finished basement, or it’s 'Unf'.
Let’s see what are the values for the 'BsmtFinType2' when the 'BsmtFinSF2' is greater than zero.
[51]:
df.loc[df['BsmtFinSF2'] > 0].groupby('MSSubClass').get_group('20')['BsmtFinType2'].value_counts()
[51]:
BsmtFinType2
Rec 29
LwQ 28
BLQ 17
ALQ 7
GLQ 5
Name: count, dtype: int64
And we see that the data should have a value that is not 'Unf'.
The problem with this row is that the mode for the finish type and the type of dwelling is actually unfinished, 'Unf', which would create a contradiction in the data. Since it is just one row I will actually drop it. In the grand scheme of things keeping this one row will not result in a large change in the final results.
[52]:
df.drop([333], inplace=True)
[53]:
missing_vals(df)
[53]:
| count | percent | |
|---|---|---|
| PoolQC | 1451 | 99.588195 |
| MiscFeature | 1403 | 96.293754 |
| Alley | 1366 | 93.754290 |
| Fence | 1176 | 80.713795 |
| FireplaceQu | 690 | 47.357584 |
| LotFrontage | 259 | 17.776253 |
| GarageType | 81 | 5.559369 |
| GarageYrBlt | 81 | 5.559369 |
| GarageFinish | 81 | 5.559369 |
| GarageQual | 81 | 5.559369 |
| GarageCond | 81 | 5.559369 |
And we have eliminated all missing data points pertaining to the basement.
Garage#
Here, I want to figure out the features pertaining to information on the garage. The values from the description file are.
GarageType: Garage location
2Types More than one type of garage
Attchd Attached to home
Basment Basement Garage
BuiltIn Built-In (Garage part of house - typically has room above garage)
CarPort Car Port
Detchd Detached from home
NA No Garage
GarageYrBlt: Year garage was built
GarageFinish: Interior finish of the garage
Fin Finished
RFn Rough Finished
Unf Unfinished
NA No Garage
GarageCars: Size of garage in car capacity
GarageArea: Size of garage in square feet
GarageQual: Garage quality
Ex Excellent
Gd Good
TA Typical/Average
Fa Fair
Po Poor
NA No Garage
GarageCond: Garage condition
Ex Excellent
Gd Good
TA Typical/Average
Fa Fair
Po Poor
NA No Garage
Let’s first take a look at the current state of the columns data.
[54]:
missing_vals(df).loc[['GarageType', 'GarageYrBlt', 'GarageFinish', 'GarageQual', 'GarageCond']]
[54]:
| count | percent | |
|---|---|---|
| GarageType | 81 | 5.559369 |
| GarageYrBlt | 81 | 5.559369 |
| GarageFinish | 81 | 5.559369 |
| GarageQual | 81 | 5.559369 |
| GarageCond | 81 | 5.559369 |
We see that the features that are missing data are all categorical features except for 'GarageYrBlt' which is for when the garage was built. However, if there is no garage then there will obviously be no year for when the garage was built.
First I want to make sure that where there is missing data the numerical values make sense.
[55]:
df.loc[df['GarageType'].isnull(), [x for x in df.columns if 'garage' in x.lower()]].value_counts(dropna=False)
[55]:
GarageType GarageYrBlt GarageFinish GarageCars GarageArea GarageQual GarageCond
NaN NaN NaN 0 0 NaN NaN 81
Name: count, dtype: int64
And clearly we see that when the categorical data is missing a value the numerical value for 'GarageCars' and 'GarageArea' is 0. For the categorical data this is a simple replacement and we will replace all Nan with 'None'.
[56]:
cat_cols = ['GarageType', 'GarageFinish', 'GarageQual', 'GarageCond']
df[cat_cols] = df[cat_cols].fillna('None')
For 'GarageYrBlt' we do not have a nice and neat value that we can asign that makes complete sense. In a way we can set the value to 0 and force it to be an outlier. It can become an interesting thought experiment to try to reason what can happen to the model when do this as opposed to setting the value to some kind of mean based on where the house is located. Could it be that by setting the values to 0 will it affect the correlation between the sale price and the year the garage was built
or if there is a garage at all.
Let’s look at that really quick. Here is the correlation between sale price and garage year before replacing the missing values.
[57]:
df.corr(numeric_only=True).loc['GarageYrBlt', 'SalePrice']
[57]:
0.4867053251422345
And if we replace the missing values with 0.
[58]:
df_tmp = df.copy()
df_tmp['GarageYrBlt'] = df_tmp['GarageYrBlt'].fillna(0)
df_tmp.corr(numeric_only=True).loc['GarageYrBlt', 'SalePrice']
[58]:
0.2613300869851237
And if we replace the missing values with 100.
[59]:
df_tmp = df.copy()
df_tmp['GarageYrBlt'] = df_tmp['GarageYrBlt'].fillna(100)
df_tmp.corr(numeric_only=True).loc['GarageYrBlt', 'SalePrice']
[59]:
0.26261306587279576
And if we replace the missing values with 1000.
[60]:
df_tmp = df.copy()
df_tmp['GarageYrBlt'] = df_tmp['GarageYrBlt'].fillna(1000)
df_tmp.corr(numeric_only=True).loc['GarageYrBlt', 'SalePrice']
[60]:
0.28550228706456937
And if we replace the missing values with 1900.
[61]:
df_tmp = df.copy()
df_tmp['GarageYrBlt'] = df_tmp['GarageYrBlt'].fillna(1900)
df_tmp.corr(numeric_only=True).loc['GarageYrBlt', 'SalePrice']
[61]:
0.5185149371069989
And if we were to replace the missing values with some average with respect to the neighborhood.
[62]:
df_tmp = df.copy()
df_tmp['GarageYrBlt'] = df_tmp.groupby('Neighborhood')['GarageYrBlt'].transform(lambda x: x.fillna(x.mean()))
df_tmp.corr(numeric_only=True).loc['GarageYrBlt', 'SalePrice']
[62]:
0.5000940244955719
I believe this is actually a peculiar problem that requires some careful consideration. We can’t just make the year a garage was built to be the average when it does not exist and is it also good to create these outliers in the data set? Well, yes actually, because it can be said that the absence of a garage is actually having a very small effect on the sale price owing to a small correlation value between them. It will be interesting to actually create a few models to see the actual effect on the final results.
For now let’s just set them to 0.
[63]:
df['GarageYrBlt'] = df['GarageYrBlt'].fillna(0)
[64]:
missing_vals(df)
[64]:
| count | percent | |
|---|---|---|
| PoolQC | 1451 | 99.588195 |
| MiscFeature | 1403 | 96.293754 |
| Alley | 1366 | 93.754290 |
| Fence | 1176 | 80.713795 |
| FireplaceQu | 690 | 47.357584 |
| LotFrontage | 259 | 17.776253 |
And we no longer have any values pertaining to the garage.
Pool quality, Alley, Fence, Misc Feature#
Let’s quickly take care of the pool quality, alley, and fence values as we already know they should be 'None' when there are missing values. As alwys I just like to be careful where I can and cross check with data that is related in the data set already. This can only be done for the 'PoolQC', and 'MiscFeature' data.
[65]:
df.loc[df['PoolQC'].isnull(), ['PoolArea', 'PoolQC']].value_counts(dropna=False)
[65]:
PoolArea PoolQC
0 NaN 1451
Name: count, dtype: int64
[66]:
df.loc[df['MiscFeature'].isnull(), ['MiscVal', 'MiscFeature']].value_counts(dropna=False)
[66]:
MiscVal MiscFeature
0 NaN 1403
Name: count, dtype: int64
[67]:
df.loc[df['FireplaceQu'].isnull(), ['Fireplaces', 'FireplaceQu']].value_counts(dropna=False)
[67]:
Fireplaces FireplaceQu
0 NaN 690
Name: count, dtype: int64
And now that we have confirmed that when 'PoolQC' is missing a value the value for 'PoolArea' is 0, we make the replacement.
[68]:
cat_cols = ['PoolQC', 'Alley', 'Fence', 'MiscFeature', 'FireplaceQu']
df[cat_cols] = df[cat_cols].fillna('None')
[69]:
missing_vals(df)
[69]:
| count | percent | |
|---|---|---|
| LotFrontage | 259 | 17.776253 |
Lot Frontage#
And we are left with dealing with missing values for the lot frontage. Here is the description for the feature.
LotFrontage: Linear feet of street connected to property
For this value we will have to go through different values and make an attempt to guess based on other values. So let’s first look at the correlation metrics as this will be a good starting point to see what values are connected.
[70]:
df.corr(numeric_only=True)['LotFrontage'].sort_values(key=abs, ascending=False).head(8)
[70]:
LotFrontage 1.000000
1stFlrSF 0.406596
LotArea 0.388597
SalePrice 0.370210
GrLivArea 0.355398
TotRmsAbvGrd 0.336123
TotalBsmtSF 0.323647
GarageArea 0.322424
Name: LotFrontage, dtype: float64
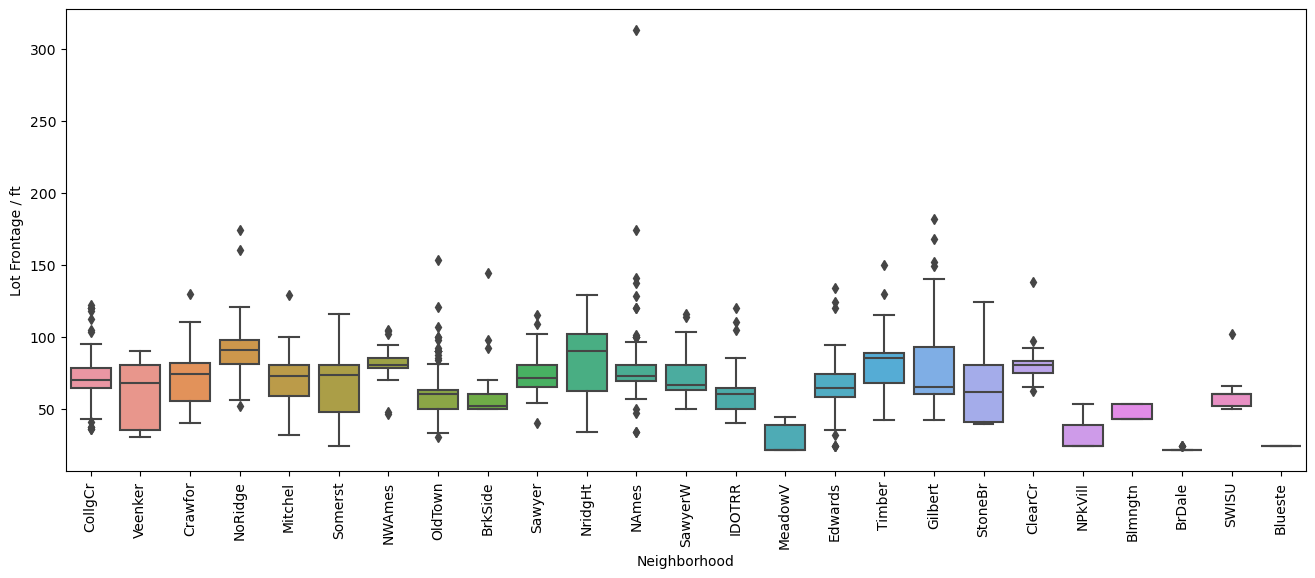
[71]:
plt.figure(figsize=(16,6), dpi=100)
sns.boxplot(y='LotFrontage', x='Neighborhood', data=df, orient='vertical')
plt.xticks(rotation=90)
plt.ylabel('Lot Frontage / ft')
[71]:
Text(0, 0.5, 'Lot Frontage / ft')
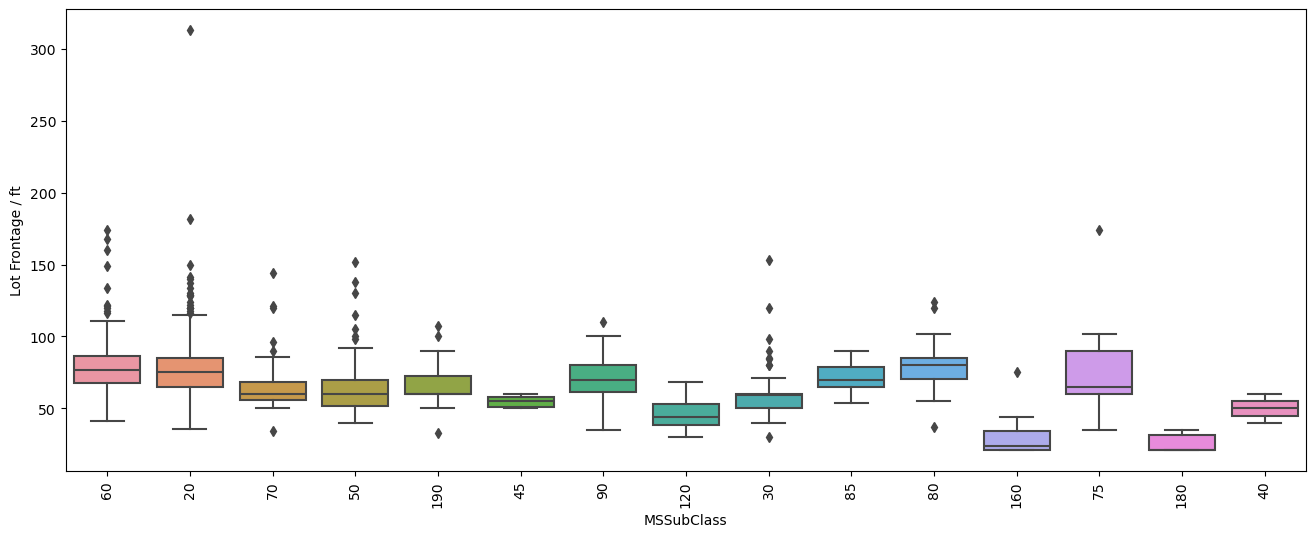
[72]:
plt.figure(figsize=(16,6), dpi=100)
sns.boxplot(y='LotFrontage', x='MSSubClass', data=df, orient='vertical')
plt.xticks(rotation=90)
plt.ylabel('Lot Frontage / ft')
[72]:
Text(0, 0.5, 'Lot Frontage / ft')
[73]:
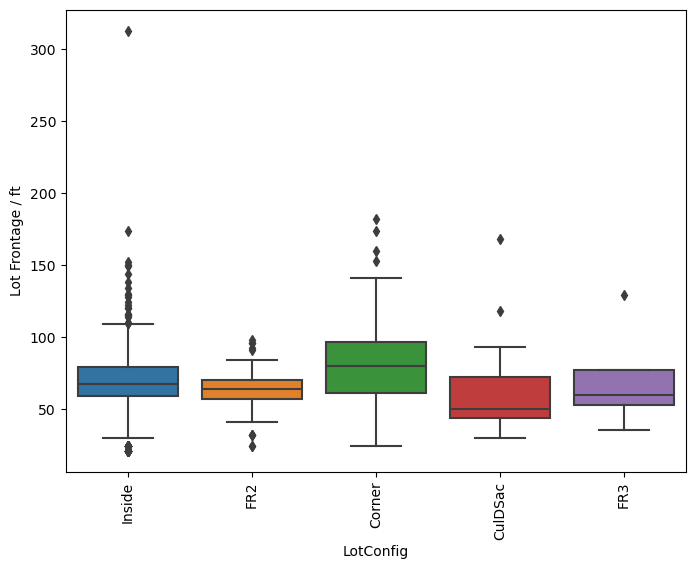
plt.figure(figsize=(8,6), dpi=100)
sns.boxplot(y='LotFrontage', x='LotConfig', data=df, orient='vertical')
plt.xticks(rotation=90)
plt.ylabel('Lot Frontage / ft')
[73]:
Text(0, 0.5, 'Lot Frontage / ft')
[74]:
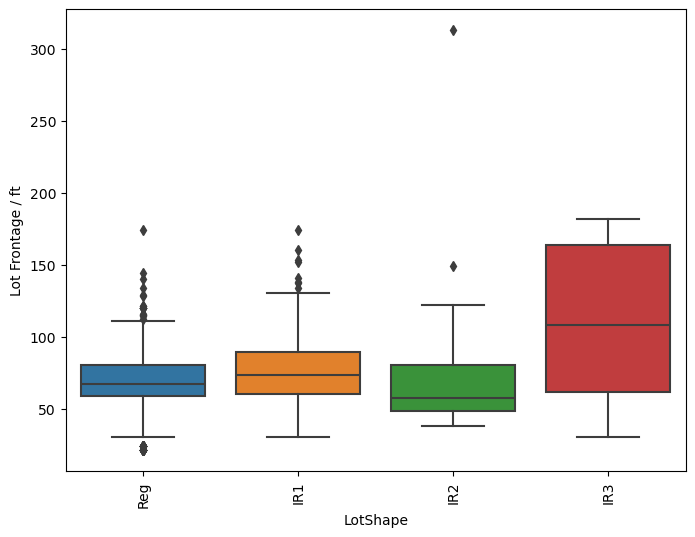
plt.figure(figsize=(8,6), dpi=100)
sns.boxplot(y='LotFrontage', x='LotShape', data=df, orient='vertical')
plt.xticks(rotation=90)
plt.ylabel('Lot Frontage / ft')
[74]:
Text(0, 0.5, 'Lot Frontage / ft')
[75]:
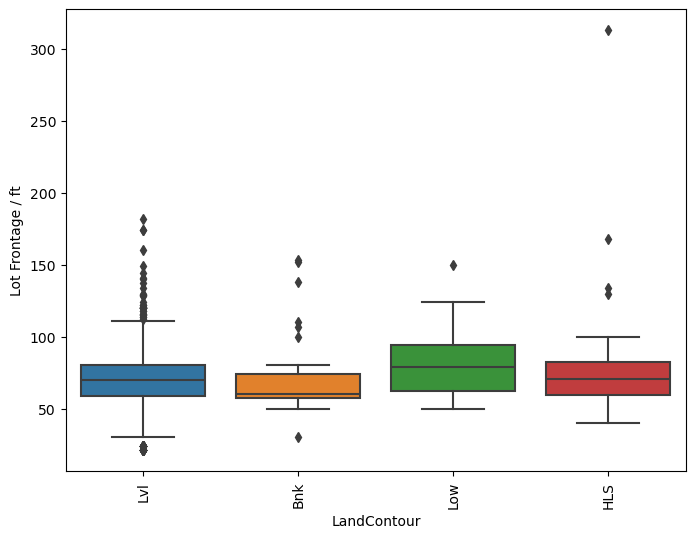
plt.figure(figsize=(8,6), dpi=100)
sns.boxplot(y='LotFrontage', x='LandContour', data=df, orient='vertical')
plt.xticks(rotation=90)
plt.ylabel('Lot Frontage / ft')
[75]:
Text(0, 0.5, 'Lot Frontage / ft')
[76]:
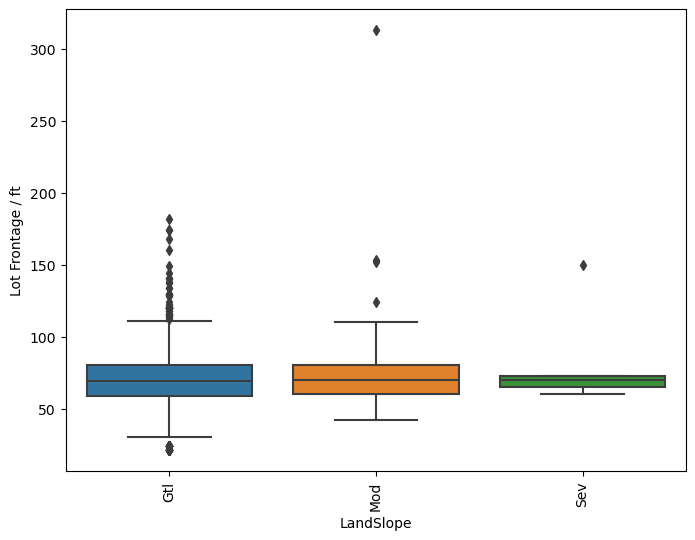
plt.figure(figsize=(8,6), dpi=100)
sns.boxplot(y='LotFrontage', x='LandSlope', data=df, orient='vertical')
plt.xticks(rotation=90)
plt.ylabel('Lot Frontage / ft')
[76]:
Text(0, 0.5, 'Lot Frontage / ft')
[77]:
sns.scatterplot(x='LotFrontage', y='1stFlrSF', data=df)
[77]:
<Axes: xlabel='LotFrontage', ylabel='1stFlrSF'>
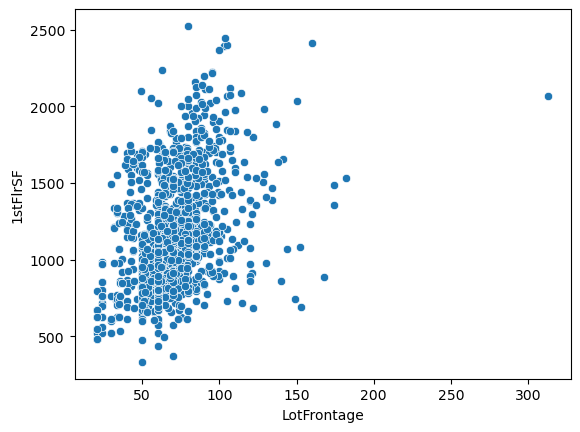
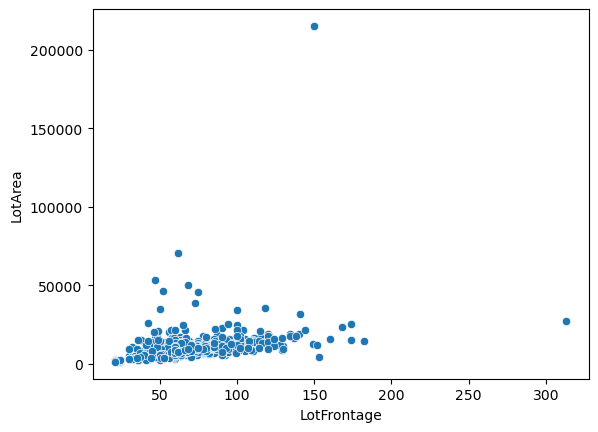
[78]:
sns.scatterplot(x='LotFrontage', y='LotArea', data=df)
[78]:
<Axes: xlabel='LotFrontage', ylabel='LotArea'>
[79]:
df.loc[df['LotArea'] > 200e3]
[79]:
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | LotConfig | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | |||||||||||||||||||||
| 314 | 20 | RL | 150.0 | 215245 | Pave | None | IR3 | Low | AllPub | Inside | ... | 0 | None | None | None | 0 | 6 | 2009 | WD | Normal | 375000 |
1 rows × 80 columns
[80]:
df.loc[df['LotFrontage'] > 300]
[80]:
| MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | LotConfig | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Id | |||||||||||||||||||||
| 935 | 20 | RL | 313.0 | 27650 | Pave | None | IR2 | HLS | AllPub | Inside | ... | 0 | None | None | None | 0 | 11 | 2008 | WD | Normal | 242000 |
1 rows × 80 columns
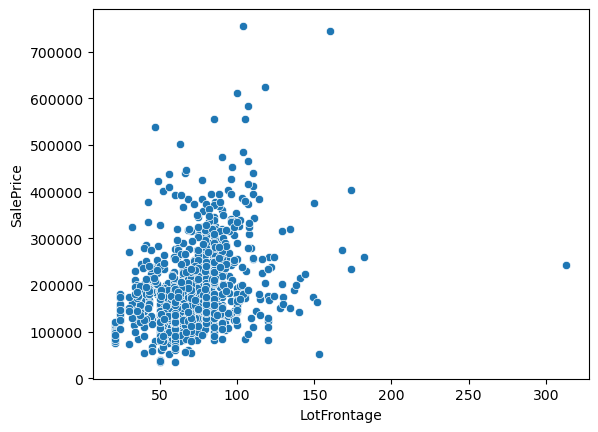
[81]:
sns.scatterplot(x='LotFrontage', y='SalePrice', data=df)
[81]:
<Axes: xlabel='LotFrontage', ylabel='SalePrice'>
So what do we see from all these plots?
Well the first one comparing the distribution of lot frontage values as a function of the neighborhood does not show a lot of variation between the values. In some neighborhoods the distribution seems to be smaller, in others there are less points that fall outside of the \(1.5\times \text{IQR}\) limits set by Seaborn in the box plots. Same applies to the next plot with dwelling types, 'MSSubClass'. It’s not until we get to comparing the values of lot area and lot frontage that we get a
good linear trend between the two values with exception of two outliers.
Based on this I will use a linear interpolation to fill in the missing values for the 'LotFrontage' column.
[82]:
def func(x, a, b):
return a*x+b
tmp = df.loc[(df['LotArea'] < 200e3) & (df['LotFrontage'] < 300)][['LotArea', 'LotFrontage']]
popt, pcov = curve_fit(f=func, xdata=tmp['LotArea'].values, ydata=tmp['LotFrontage'].values)
Before we make the replacement lets take a look at how the line fit looks.
[83]:
sns.scatterplot(y='LotFrontage', x='LotArea', data=tmp)
x = np.linspace(0, 70e3, 20)
plt.plot(x, func(x, *popt), color='tab:red', linestyle='--')
[83]:
[<matplotlib.lines.Line2D at 0x1c879d69650>]
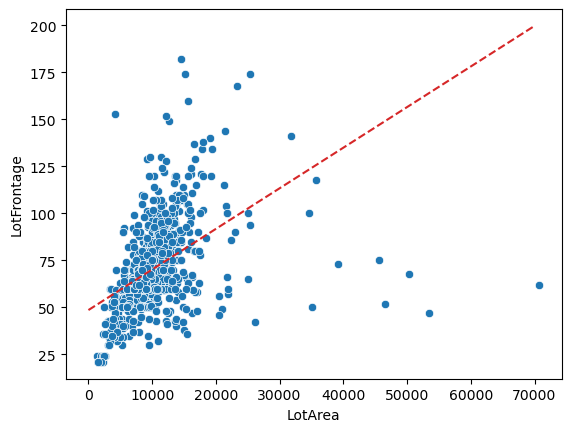
That’s a pretty terrible fit. Due to this issue we will have to use another method to impute the values.
Based on the previous plots we see that there is a small dependence on the lot frontage values on which neighborhood we are in. So let’s take a look at the averages that we can get only from the neighborhoods and try to mix it up invloving the type of dwelling 'MSSubClass', lot configuration 'LotConfig', or 'LotShape'.
[84]:
sns.scatterplot(y='LotFrontage', x='SalePrice', data=df)
[84]:
<Axes: xlabel='SalePrice', ylabel='LotFrontage'>
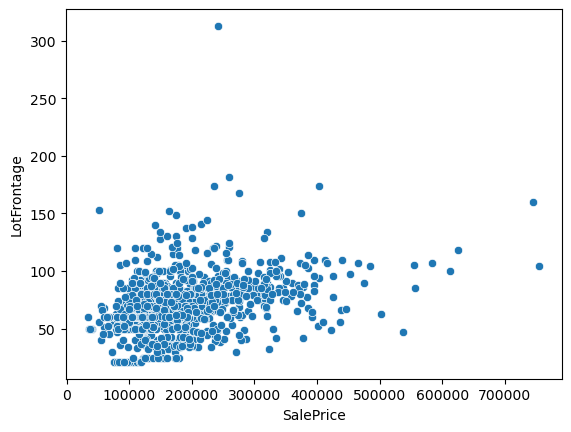
Group by the 'Neighborhood' column and transform missing values (orange markers) with the average or median.
[85]:
gen_lotfront_plot(df, 'Neighborhood')
Missing values after average: 0
Missing values after median: 0
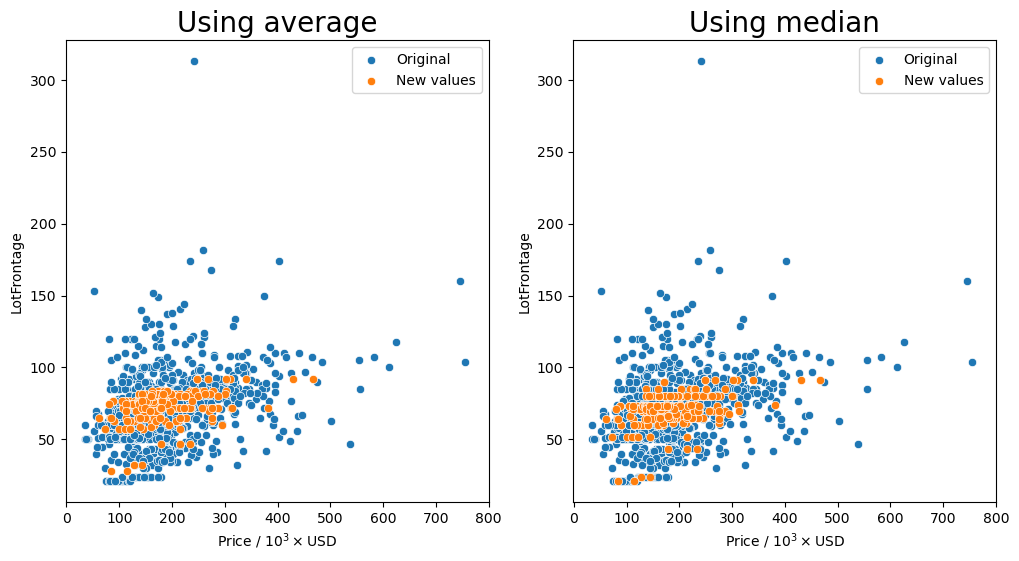
Group by the 'Neighborhood', 'MSSubClass', and 'MSZoning' columns and transform missing values (orange markers) with the average or median.
[86]:
gen_lotfront_plot(df, ['Neighborhood', 'MSSubClass', 'MSZoning'])
Missing values after average: 11
Missing values after median: 11
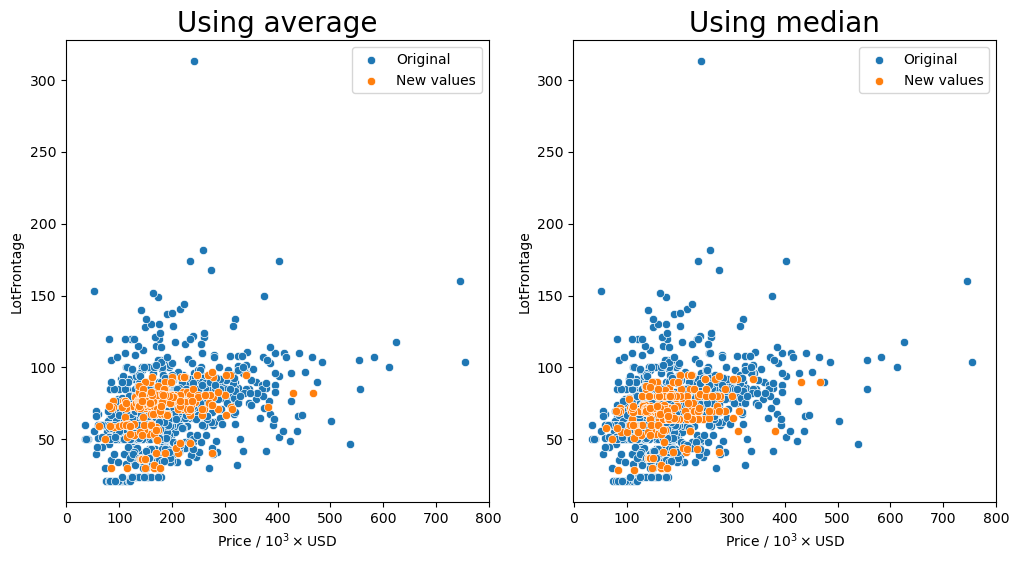
Group by the 'LontConfig', and 'LotShape' columns and transform missing values (orange markers) with the average or median.
[87]:
gen_lotfront_plot(df, ['LotConfig', 'LotShape'])
Missing values after average: 1
Missing values after median: 1
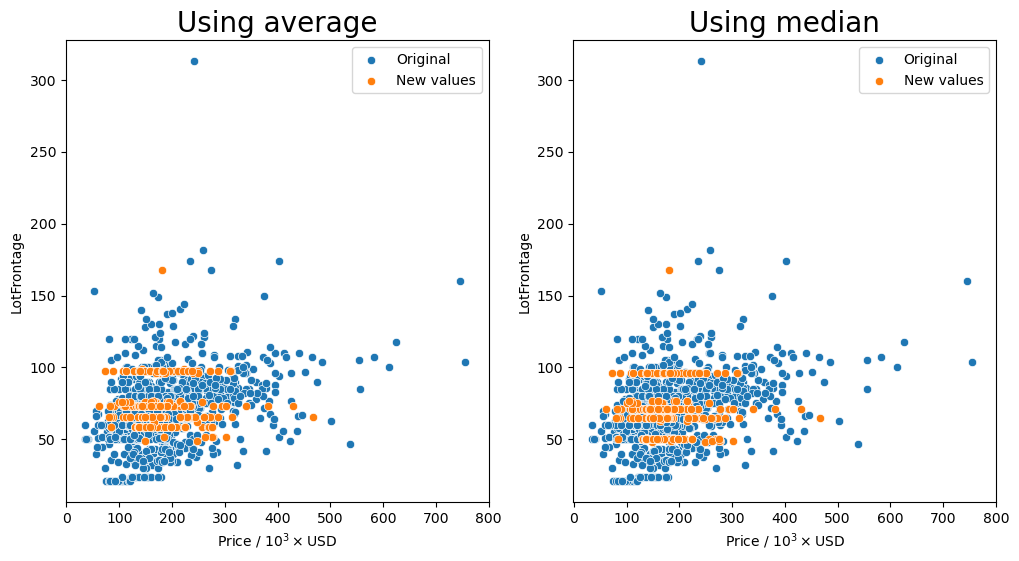
Group by the 'Neighborhood', 'LontConfig', and 'LotShape' columns and transform missing values (orange markers) with the average or median.
[88]:
gen_lotfront_plot(df, ['LotConfig', 'LotShape', 'Neighborhood'])
Missing values after average: 33
Missing values after median: 33
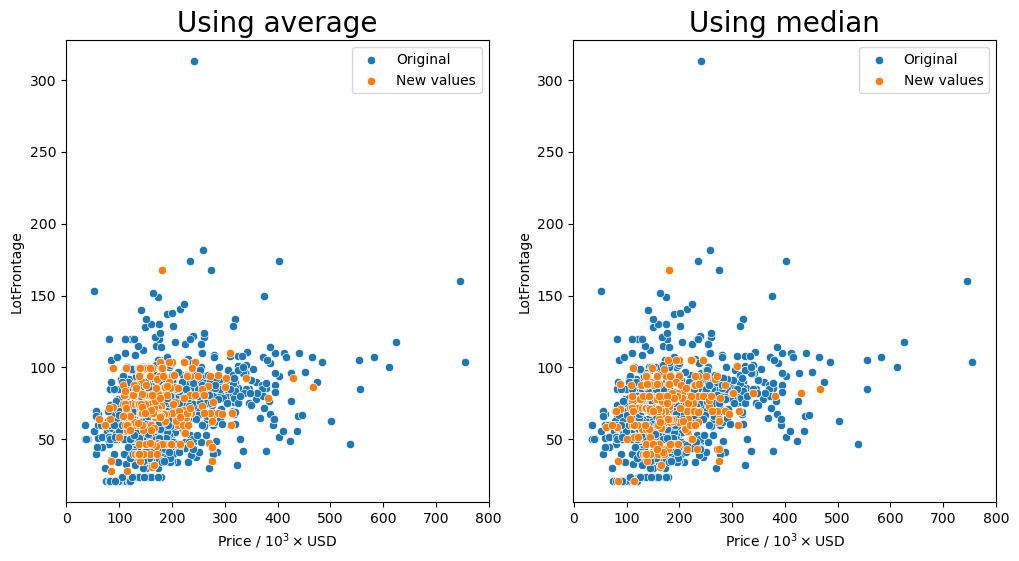
Group by the 'LandContour', and 'LotShape' columns and transform missing values (orange markers) with the average or median.
[89]:
gen_lotfront_plot(df, ['LandContour', 'LotShape'])
Missing values after average: 0
Missing values after median: 0
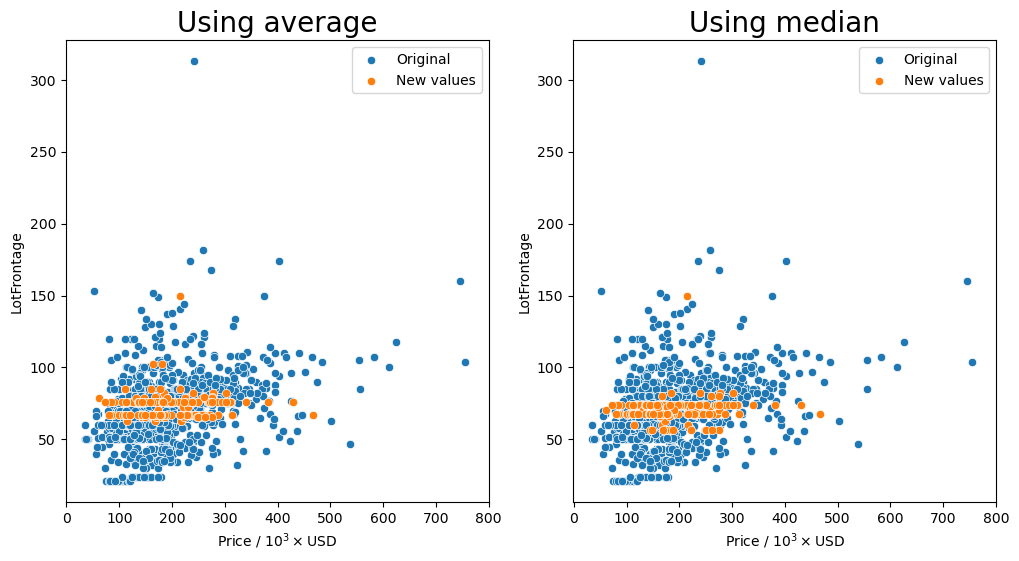
Group by the 'Neighborhood', 'LandContour', and 'LotShape' columns and transform missing values (orange markers) with the average or median.
[90]:
gen_lotfront_plot(df, ['LandContour', 'LotShape', 'Neighborhood'])
Missing values after average: 21
Missing values after median: 21
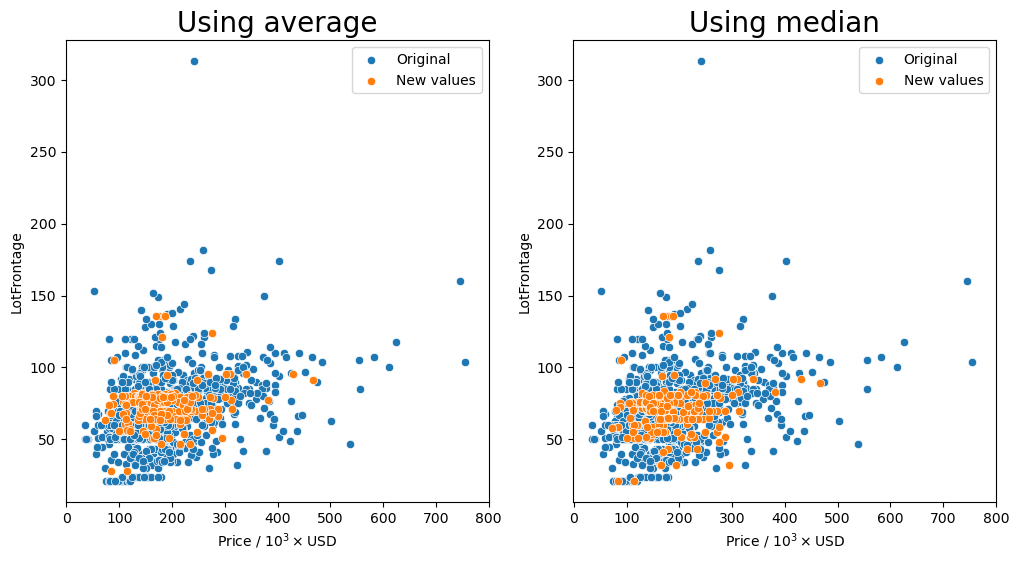
It seems that for most of the combinations that we tried for how to group the values, having the 'Neighborhood' column in the group seemed to keep the resulting values fairly consistent as shown by the orange markers. We see that they are spread out throughout the entire middle section with most of the other data points.
So the question remains, which is the best method? Just transforming the missing values in the data set with the average for each neighborhood seems to behave well enough as we have seen that there is a small dependence on the lot frontage and the neighborhood. However, I would argue that the shape and the configuration of the lot are equally as important. We can see in the box plots that the distribution of lot frontage values with respect to the lot configuration ('LotConfig') and lot
shape ('LotShape') does vary from one to the other. The 'IR3' values in 'LotShape' have a very wide distribution and it makes sense to separate those values from the rest as it can affect the average that is calculated.
As always this is mainly just an educated guess on what is the best method to deal with the missing numerical values. I believe that this method tries to take many different parameters that can affect the lot frontage value and gives a more realistic value. You will always have outliers, but I think this is the best that we can some up with.
So I will make the replacement of the missing values with a transformed average after grouping by 'Neighborhood', 'LotConfig', and 'LotShape'. But, there is one big issue with this. There are still missing values in the 'LotFrontage' column meaning that there are not enough data points in the groups to calculate the average this way. Seeing as grouping by just the 'Neighborhood' fills in all the missing values, I will just group by the 'Neighborhood' column and fill
in the calculated average.
[91]:
group_cols = ['Neighborhood']
df['LotFrontage'] = df.groupby(group_cols)['LotFrontage'].transform(lambda x: x.fillna(x.mean()))
[92]:
missing_vals(df)
[92]:
| count | percent |
|---|
And we are done replacing all of the missing values in the data set and can start to actually use it for predictions!!
[93]:
df_objs = df.select_dtypes(include='object')
df_nums = df.select_dtypes(exclude='object')
[94]:
df_objs.info()
<class 'pandas.core.frame.DataFrame'>
Index: 1457 entries, 1 to 1460
Data columns (total 44 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 MSSubClass 1457 non-null object
1 MSZoning 1457 non-null object
2 Street 1457 non-null object
3 Alley 1457 non-null object
4 LotShape 1457 non-null object
5 LandContour 1457 non-null object
6 Utilities 1457 non-null object
7 LotConfig 1457 non-null object
8 LandSlope 1457 non-null object
9 Neighborhood 1457 non-null object
10 Condition1 1457 non-null object
11 Condition2 1457 non-null object
12 BldgType 1457 non-null object
13 HouseStyle 1457 non-null object
14 RoofStyle 1457 non-null object
15 RoofMatl 1457 non-null object
16 Exterior1st 1457 non-null object
17 Exterior2nd 1457 non-null object
18 MasVnrType 1457 non-null object
19 ExterQual 1457 non-null object
20 ExterCond 1457 non-null object
21 Foundation 1457 non-null object
22 BsmtQual 1457 non-null object
23 BsmtCond 1457 non-null object
24 BsmtExposure 1457 non-null object
25 BsmtFinType1 1457 non-null object
26 BsmtFinType2 1457 non-null object
27 Heating 1457 non-null object
28 HeatingQC 1457 non-null object
29 CentralAir 1457 non-null object
30 Electrical 1457 non-null object
31 KitchenQual 1457 non-null object
32 Functional 1457 non-null object
33 FireplaceQu 1457 non-null object
34 GarageType 1457 non-null object
35 GarageFinish 1457 non-null object
36 GarageQual 1457 non-null object
37 GarageCond 1457 non-null object
38 PavedDrive 1457 non-null object
39 PoolQC 1457 non-null object
40 Fence 1457 non-null object
41 MiscFeature 1457 non-null object
42 SaleType 1457 non-null object
43 SaleCondition 1457 non-null object
dtypes: object(44)
memory usage: 512.2+ KB
[95]:
df_nums.info()
<class 'pandas.core.frame.DataFrame'>
Index: 1457 entries, 1 to 1460
Data columns (total 36 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 LotFrontage 1457 non-null float64
1 LotArea 1457 non-null int64
2 OverallQual 1457 non-null int64
3 OverallCond 1457 non-null int64
4 YearBuilt 1457 non-null int64
5 YearRemodAdd 1457 non-null int64
6 MasVnrArea 1457 non-null float64
7 BsmtFinSF1 1457 non-null int64
8 BsmtFinSF2 1457 non-null int64
9 BsmtUnfSF 1457 non-null int64
10 TotalBsmtSF 1457 non-null int64
11 1stFlrSF 1457 non-null int64
12 2ndFlrSF 1457 non-null int64
13 LowQualFinSF 1457 non-null int64
14 GrLivArea 1457 non-null int64
15 BsmtFullBath 1457 non-null int64
16 BsmtHalfBath 1457 non-null int64
17 FullBath 1457 non-null int64
18 HalfBath 1457 non-null int64
19 BedroomAbvGr 1457 non-null int64
20 KitchenAbvGr 1457 non-null int64
21 TotRmsAbvGrd 1457 non-null int64
22 Fireplaces 1457 non-null int64
23 GarageYrBlt 1457 non-null float64
24 GarageCars 1457 non-null int64
25 GarageArea 1457 non-null int64
26 WoodDeckSF 1457 non-null int64
27 OpenPorchSF 1457 non-null int64
28 EnclosedPorch 1457 non-null int64
29 3SsnPorch 1457 non-null int64
30 ScreenPorch 1457 non-null int64
31 PoolArea 1457 non-null int64
32 MiscVal 1457 non-null int64
33 MoSold 1457 non-null int64
34 YrSold 1457 non-null int64
35 SalePrice 1457 non-null int64
dtypes: float64(3), int64(33)
memory usage: 421.2 KB
[96]:
df_objs = pd.get_dummies(df_objs, drop_first=True)
Save the final data set after processing#
[97]:
final_df = pd.concat([df_nums, df_objs], axis=1)
[98]:
final_df.to_csv(os.path.join('_data', 'ames-data-no-missing.csv'))
Linear Regression#
Import linear regression libraries#
[99]:
from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV, ElasticNetCV
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn import metrics
[100]:
def convert_strings(num, base):
length = int(np.floor(np.log10(num)))
if length < base:
s = '0'+str(round(num, -(base-2)))[:2]
elif length == base:
s = str(round(num, -(base-2)))[:3]
else:
raise ValueError('The length of the number to round is larger')
return '{}.{}E+{:02d}'.format(s[0], s[1:], base)
def gen_comp_plot(title, pred, test, ax, avg, metrics, alpha=0.3, text_tmp=None):
if text_tmp is None:
text_tmp = error_text
base = int(np.floor(np.log10(avg_price)))
str_vals = [convert_strings(avg, base),
convert_strings(metrics['MAE'], base),
convert_strings(metrics['MedAE'], base),
convert_strings(metrics['RMSE'], base),
metrics['r2']]
sns.scatterplot(x=test, y=pred, alpha=0.3, ax=ax)
replace_price_ticks(ax, True, 'Actual sale price')
replace_price_ticks(ax, False, 'Predicted sale price')
ylim = ax.get_ylim()
xlim = ax.get_xlim()
new_lim = list(ylim)
if new_lim[0] > xlim[0]:
new_lim[0] = xlim[0]
if new_lim[1] < xlim[1]:
new_lim[1] = xlim[1]
ax.set_ylim(new_lim)
ax.set_xlim(new_lim)
ax.plot(new_lim, new_lim, color='tab:red', linestyle='--')
ax.text(s=text_tmp.format(*str_vals),
x=0.025, y=0.97, transform=ax.transAxes, ha='left', va='top',
bbox=dict(fc="none"))
ax.set_title(title)
[101]:
error_text = '''\
- Average sale price: {}
- Mean absolute error: {}
- Median absolute error: {}
- Root mean squared error: {}
- R Squared: {:.4f}\
'''
errors = {}
alphas = {}
test_preds = {}
models = {}
Data manipulation#
[102]:
dtypes = dict(MSSubClass=str)
df = pd.read_csv(os.path.join('_data', 'ames-data-no-missing.csv'), index_col=0)
[103]:
np.where(df.isnull().any())
[103]:
(array([], dtype=int64),)
Make a train test split#
[104]:
X = df.drop('SalePrice', axis=1)
y = df['SalePrice']
[105]:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=42)
avg_price = y_test.mean()
Scale the data#
[106]:
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
Ordinary least squares#
[107]:
model = LinearRegression()
[108]:
model.fit(X_train, y_train)
models['ols'] = model
[109]:
test_predictions = models['ols'].predict(X_test)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
test_preds['ols'] = test_predictions
errors['ols'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
MedAE=MedAE, r2=r2)
Plotting real vs. predicted values#
[110]:
fig, ax = plt.subplots()
gen_comp_plot('Ordinary Least Squares', test_preds['ols'], y_test, ax,
avg_price, errors['ols'])
fig.tight_layout()
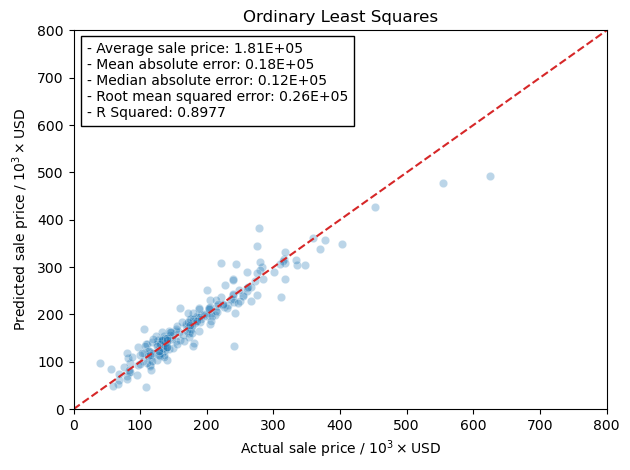
Ridge Regression#
Now I will use the scaled training data and train the models using the RidgeCV model in the linear_regression module in scikit-learn. This will let me more easily tune the hyper-parameter, \(\alpha\), rather than running a grid search. The reason I am doing this is that RidgeCV will use a scoring function to determine the best hyper-parameter. This is more of a curiosity of mine to see how the scoring actually affects the final results from training the model.
[111]:
models['ridge'] = {}
errors['ridge'] = {}
test_preds['ridge'] = {}
Mean Absolute Error#
Here we use the mean absolute error as the scoring metric in the training step.
[112]:
model = RidgeCV(alphas=np.arange(350, 360, 0.05), scoring='neg_mean_absolute_error')
[113]:
model.fit(X_train_scaled, y_train)
[113]:
RidgeCV(alphas=array([350. , 350.05, 350.1 , 350.15, 350.2 , 350.25, 350.3 , 350.35,
350.4 , 350.45, 350.5 , 350.55, 350.6 , 350.65, 350.7 , 350.75,
350.8 , 350.85, 350.9 , 350.95, 351. , 351.05, 351.1 , 351.15,
351.2 , 351.25, 351.3 , 351.35, 351.4 , 351.45, 351.5 , 351.55,
351.6 , 351.65, 351.7 , 351.75, 351.8 , 351.85, 351.9 , 351.95,
352. , 352.05, 352.1 , 352.15, 352.2 , 352.25, 352.3 , 352.35,
352.4 , 352.45, 352.5 ,...
357.2 , 357.25, 357.3 , 357.35, 357.4 , 357.45, 357.5 , 357.55,
357.6 , 357.65, 357.7 , 357.75, 357.8 , 357.85, 357.9 , 357.95,
358. , 358.05, 358.1 , 358.15, 358.2 , 358.25, 358.3 , 358.35,
358.4 , 358.45, 358.5 , 358.55, 358.6 , 358.65, 358.7 , 358.75,
358.8 , 358.85, 358.9 , 358.95, 359. , 359.05, 359.1 , 359.15,
359.2 , 359.25, 359.3 , 359.35, 359.4 , 359.45, 359.5 , 359.55,
359.6 , 359.65, 359.7 , 359.75, 359.8 , 359.85, 359.9 , 359.95]),
scoring='neg_mean_absolute_error')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
RidgeCV(alphas=array([350. , 350.05, 350.1 , 350.15, 350.2 , 350.25, 350.3 , 350.35,
350.4 , 350.45, 350.5 , 350.55, 350.6 , 350.65, 350.7 , 350.75,
350.8 , 350.85, 350.9 , 350.95, 351. , 351.05, 351.1 , 351.15,
351.2 , 351.25, 351.3 , 351.35, 351.4 , 351.45, 351.5 , 351.55,
351.6 , 351.65, 351.7 , 351.75, 351.8 , 351.85, 351.9 , 351.95,
352. , 352.05, 352.1 , 352.15, 352.2 , 352.25, 352.3 , 352.35,
352.4 , 352.45, 352.5 ,...
357.2 , 357.25, 357.3 , 357.35, 357.4 , 357.45, 357.5 , 357.55,
357.6 , 357.65, 357.7 , 357.75, 357.8 , 357.85, 357.9 , 357.95,
358. , 358.05, 358.1 , 358.15, 358.2 , 358.25, 358.3 , 358.35,
358.4 , 358.45, 358.5 , 358.55, 358.6 , 358.65, 358.7 , 358.75,
358.8 , 358.85, 358.9 , 358.95, 359. , 359.05, 359.1 , 359.15,
359.2 , 359.25, 359.3 , 359.35, 359.4 , 359.45, 359.5 , 359.55,
359.6 , 359.65, 359.7 , 359.75, 359.8 , 359.85, 359.9 , 359.95]),
scoring='neg_mean_absolute_error')[114]:
models['ridge']['MAE'] = model
alphas['MAE'] = model.alpha_
model.alpha_
[114]:
354.500000000001
[115]:
test_predictions = models['ridge']['MAE'].predict(X_test_scaled)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
MAPerE = metrics.mean_absolute_percentage_error(y_test, test_predictions)
errors['ridge']['MAE'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
r2=r2, MedAE=MedAE, MAPerE=MAPerE)
test_preds['ridge']['MAE'] = test_predictions
Mean Squared Error or Root Mean Squared Error#
Here we use the mean squared error as the scoring metric in the training step. According to the documentation on scikit-learn, if you want to use the root mean squared error as the scoring metric you end up just using mean squared error. Which makes sense honestly.
[116]:
model = RidgeCV(alphas=np.arange(185, 195, 0.05), scoring='neg_mean_squared_error')
[117]:
model.fit(X_train_scaled, y_train)
[117]:
RidgeCV(alphas=array([185. , 185.05, 185.1 , 185.15, 185.2 , 185.25, 185.3 , 185.35,
185.4 , 185.45, 185.5 , 185.55, 185.6 , 185.65, 185.7 , 185.75,
185.8 , 185.85, 185.9 , 185.95, 186. , 186.05, 186.1 , 186.15,
186.2 , 186.25, 186.3 , 186.35, 186.4 , 186.45, 186.5 , 186.55,
186.6 , 186.65, 186.7 , 186.75, 186.8 , 186.85, 186.9 , 186.95,
187. , 187.05, 187.1 , 187.15, 187.2 , 187.25, 187.3 , 187.35,
187.4 , 187.45, 187.5 ,...
192.2 , 192.25, 192.3 , 192.35, 192.4 , 192.45, 192.5 , 192.55,
192.6 , 192.65, 192.7 , 192.75, 192.8 , 192.85, 192.9 , 192.95,
193. , 193.05, 193.1 , 193.15, 193.2 , 193.25, 193.3 , 193.35,
193.4 , 193.45, 193.5 , 193.55, 193.6 , 193.65, 193.7 , 193.75,
193.8 , 193.85, 193.9 , 193.95, 194. , 194.05, 194.1 , 194.15,
194.2 , 194.25, 194.3 , 194.35, 194.4 , 194.45, 194.5 , 194.55,
194.6 , 194.65, 194.7 , 194.75, 194.8 , 194.85, 194.9 , 194.95]),
scoring='neg_mean_squared_error')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
RidgeCV(alphas=array([185. , 185.05, 185.1 , 185.15, 185.2 , 185.25, 185.3 , 185.35,
185.4 , 185.45, 185.5 , 185.55, 185.6 , 185.65, 185.7 , 185.75,
185.8 , 185.85, 185.9 , 185.95, 186. , 186.05, 186.1 , 186.15,
186.2 , 186.25, 186.3 , 186.35, 186.4 , 186.45, 186.5 , 186.55,
186.6 , 186.65, 186.7 , 186.75, 186.8 , 186.85, 186.9 , 186.95,
187. , 187.05, 187.1 , 187.15, 187.2 , 187.25, 187.3 , 187.35,
187.4 , 187.45, 187.5 ,...
192.2 , 192.25, 192.3 , 192.35, 192.4 , 192.45, 192.5 , 192.55,
192.6 , 192.65, 192.7 , 192.75, 192.8 , 192.85, 192.9 , 192.95,
193. , 193.05, 193.1 , 193.15, 193.2 , 193.25, 193.3 , 193.35,
193.4 , 193.45, 193.5 , 193.55, 193.6 , 193.65, 193.7 , 193.75,
193.8 , 193.85, 193.9 , 193.95, 194. , 194.05, 194.1 , 194.15,
194.2 , 194.25, 194.3 , 194.35, 194.4 , 194.45, 194.5 , 194.55,
194.6 , 194.65, 194.7 , 194.75, 194.8 , 194.85, 194.9 , 194.95]),
scoring='neg_mean_squared_error')[118]:
models['ridge']['MSE'] = model
alphas['MSE'] = model.alpha_
model.alpha_
[118]:
190.15000000000117
[119]:
test_predictions = models['ridge']['MSE'].predict(X_test_scaled)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
MAPerE = metrics.mean_absolute_percentage_error(y_test, test_predictions)
errors['ridge']['MSE'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
r2=r2, MedAE=MedAE, MAPerE=MAPerE)
errors['ridge']['RMSE'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
r2=r2, MedAE=MedAE, MAPerE=MAPerE)
test_preds['ridge']['MSE'] = test_predictions
R Squared (coefficient of determination)#
Here we use R squared as the scoring metric in the training step.
[120]:
model = RidgeCV(alphas=np.arange(185, 195, 0.05), scoring='r2')
[121]:
model.fit(X_train_scaled, y_train)
[121]:
RidgeCV(alphas=array([185. , 185.05, 185.1 , 185.15, 185.2 , 185.25, 185.3 , 185.35,
185.4 , 185.45, 185.5 , 185.55, 185.6 , 185.65, 185.7 , 185.75,
185.8 , 185.85, 185.9 , 185.95, 186. , 186.05, 186.1 , 186.15,
186.2 , 186.25, 186.3 , 186.35, 186.4 , 186.45, 186.5 , 186.55,
186.6 , 186.65, 186.7 , 186.75, 186.8 , 186.85, 186.9 , 186.95,
187. , 187.05, 187.1 , 187.15, 187.2 , 187.25, 187.3 , 187.35,
187.4 , 187.45, 187.5 ,...
192.2 , 192.25, 192.3 , 192.35, 192.4 , 192.45, 192.5 , 192.55,
192.6 , 192.65, 192.7 , 192.75, 192.8 , 192.85, 192.9 , 192.95,
193. , 193.05, 193.1 , 193.15, 193.2 , 193.25, 193.3 , 193.35,
193.4 , 193.45, 193.5 , 193.55, 193.6 , 193.65, 193.7 , 193.75,
193.8 , 193.85, 193.9 , 193.95, 194. , 194.05, 194.1 , 194.15,
194.2 , 194.25, 194.3 , 194.35, 194.4 , 194.45, 194.5 , 194.55,
194.6 , 194.65, 194.7 , 194.75, 194.8 , 194.85, 194.9 , 194.95]),
scoring='r2')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
RidgeCV(alphas=array([185. , 185.05, 185.1 , 185.15, 185.2 , 185.25, 185.3 , 185.35,
185.4 , 185.45, 185.5 , 185.55, 185.6 , 185.65, 185.7 , 185.75,
185.8 , 185.85, 185.9 , 185.95, 186. , 186.05, 186.1 , 186.15,
186.2 , 186.25, 186.3 , 186.35, 186.4 , 186.45, 186.5 , 186.55,
186.6 , 186.65, 186.7 , 186.75, 186.8 , 186.85, 186.9 , 186.95,
187. , 187.05, 187.1 , 187.15, 187.2 , 187.25, 187.3 , 187.35,
187.4 , 187.45, 187.5 ,...
192.2 , 192.25, 192.3 , 192.35, 192.4 , 192.45, 192.5 , 192.55,
192.6 , 192.65, 192.7 , 192.75, 192.8 , 192.85, 192.9 , 192.95,
193. , 193.05, 193.1 , 193.15, 193.2 , 193.25, 193.3 , 193.35,
193.4 , 193.45, 193.5 , 193.55, 193.6 , 193.65, 193.7 , 193.75,
193.8 , 193.85, 193.9 , 193.95, 194. , 194.05, 194.1 , 194.15,
194.2 , 194.25, 194.3 , 194.35, 194.4 , 194.45, 194.5 , 194.55,
194.6 , 194.65, 194.7 , 194.75, 194.8 , 194.85, 194.9 , 194.95]),
scoring='r2')[122]:
models['ridge']['r2'] = model
alphas['r2'] = model.alpha_
model.alpha_
[122]:
190.15000000000117
[123]:
test_predictions = models['ridge']['r2'].predict(X_test_scaled)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
MAPerE = metrics.mean_absolute_percentage_error(y_test, test_predictions)
errors['ridge']['r2'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
r2=r2, MedAE=MedAE, MAPerE=MAPerE)
print(error_text.format(y_test.mean(), MAE, RMSE, MedAE, r2))
test_preds['ridge']['r2'] = test_predictions
- Average sale price: 181122.35616438356
- Mean absolute error: 17800.40465778638
- Median absolute error: 26864.900197008257
- Root mean squared error: 12640.520799038932
- R Squared: 0.8909
Median Absolute Error#
Here we use the median absolute error as the scoring metric in the training step.
[124]:
model = RidgeCV(alphas=np.arange(740, 750, 0.05), scoring='neg_median_absolute_error')
[125]:
model.fit(X_train_scaled, y_train)
[125]:
RidgeCV(alphas=array([740. , 740.05, 740.1 , 740.15, 740.2 , 740.25, 740.3 , 740.35,
740.4 , 740.45, 740.5 , 740.55, 740.6 , 740.65, 740.7 , 740.75,
740.8 , 740.85, 740.9 , 740.95, 741. , 741.05, 741.1 , 741.15,
741.2 , 741.25, 741.3 , 741.35, 741.4 , 741.45, 741.5 , 741.55,
741.6 , 741.65, 741.7 , 741.75, 741.8 , 741.85, 741.9 , 741.95,
742. , 742.05, 742.1 , 742.15, 742.2 , 742.25, 742.3 , 742.35,
742.4 , 742.45, 742.5 ,...
747.2 , 747.25, 747.3 , 747.35, 747.4 , 747.45, 747.5 , 747.55,
747.6 , 747.65, 747.7 , 747.75, 747.8 , 747.85, 747.9 , 747.95,
748. , 748.05, 748.1 , 748.15, 748.2 , 748.25, 748.3 , 748.35,
748.4 , 748.45, 748.5 , 748.55, 748.6 , 748.65, 748.7 , 748.75,
748.8 , 748.85, 748.9 , 748.95, 749. , 749.05, 749.1 , 749.15,
749.2 , 749.25, 749.3 , 749.35, 749.4 , 749.45, 749.5 , 749.55,
749.6 , 749.65, 749.7 , 749.75, 749.8 , 749.85, 749.9 , 749.95]),
scoring='neg_median_absolute_error')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
RidgeCV(alphas=array([740. , 740.05, 740.1 , 740.15, 740.2 , 740.25, 740.3 , 740.35,
740.4 , 740.45, 740.5 , 740.55, 740.6 , 740.65, 740.7 , 740.75,
740.8 , 740.85, 740.9 , 740.95, 741. , 741.05, 741.1 , 741.15,
741.2 , 741.25, 741.3 , 741.35, 741.4 , 741.45, 741.5 , 741.55,
741.6 , 741.65, 741.7 , 741.75, 741.8 , 741.85, 741.9 , 741.95,
742. , 742.05, 742.1 , 742.15, 742.2 , 742.25, 742.3 , 742.35,
742.4 , 742.45, 742.5 ,...
747.2 , 747.25, 747.3 , 747.35, 747.4 , 747.45, 747.5 , 747.55,
747.6 , 747.65, 747.7 , 747.75, 747.8 , 747.85, 747.9 , 747.95,
748. , 748.05, 748.1 , 748.15, 748.2 , 748.25, 748.3 , 748.35,
748.4 , 748.45, 748.5 , 748.55, 748.6 , 748.65, 748.7 , 748.75,
748.8 , 748.85, 748.9 , 748.95, 749. , 749.05, 749.1 , 749.15,
749.2 , 749.25, 749.3 , 749.35, 749.4 , 749.45, 749.5 , 749.55,
749.6 , 749.65, 749.7 , 749.75, 749.8 , 749.85, 749.9 , 749.95]),
scoring='neg_median_absolute_error')[126]:
models['ridge']['MedAE'] = model
alphas['MedAE'] = model.alpha_
model.alpha_
[126]:
748.799999999992
[127]:
test_predictions = models['ridge']['MedAE'].predict(X_test_scaled)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
MAPerE = metrics.mean_absolute_percentage_error(y_test, test_predictions)
errors['ridge']['MedAE'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
r2=r2, MedAE=MedAE, MAPerE=MAPerE)
test_preds['ridge']['MedAE'] = test_predictions
Mean Absolute Percentage Error#
Here we use the mean absolute percentage error as the scoring metric in the training step.
[128]:
model = RidgeCV(alphas=np.arange(1020, 1030, 0.05), scoring='neg_mean_absolute_percentage_error')
[129]:
model.fit(X_train_scaled, y_train)
[129]:
RidgeCV(alphas=array([1020. , 1020.05, 1020.1 , 1020.15, 1020.2 , 1020.25, 1020.3 ,
1020.35, 1020.4 , 1020.45, 1020.5 , 1020.55, 1020.6 , 1020.65,
1020.7 , 1020.75, 1020.8 , 1020.85, 1020.9 , 1020.95, 1021. ,
1021.05, 1021.1 , 1021.15, 1021.2 , 1021.25, 1021.3 , 1021.35,
1021.4 , 1021.45, 1021.5 , 1021.55, 1021.6 , 1021.65, 1021.7 ,
1021.75, 1021.8 , 1021.85, 1021.9 , 1021.95, 1022. , 1022.05,
1022.1 , 1022.15, 1...
1027.7 , 1027.75, 1027.8 , 1027.85, 1027.9 , 1027.95, 1028. ,
1028.05, 1028.1 , 1028.15, 1028.2 , 1028.25, 1028.3 , 1028.35,
1028.4 , 1028.45, 1028.5 , 1028.55, 1028.6 , 1028.65, 1028.7 ,
1028.75, 1028.8 , 1028.85, 1028.9 , 1028.95, 1029. , 1029.05,
1029.1 , 1029.15, 1029.2 , 1029.25, 1029.3 , 1029.35, 1029.4 ,
1029.45, 1029.5 , 1029.55, 1029.6 , 1029.65, 1029.7 , 1029.75,
1029.8 , 1029.85, 1029.9 , 1029.95]),
scoring='neg_mean_absolute_percentage_error')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
RidgeCV(alphas=array([1020. , 1020.05, 1020.1 , 1020.15, 1020.2 , 1020.25, 1020.3 ,
1020.35, 1020.4 , 1020.45, 1020.5 , 1020.55, 1020.6 , 1020.65,
1020.7 , 1020.75, 1020.8 , 1020.85, 1020.9 , 1020.95, 1021. ,
1021.05, 1021.1 , 1021.15, 1021.2 , 1021.25, 1021.3 , 1021.35,
1021.4 , 1021.45, 1021.5 , 1021.55, 1021.6 , 1021.65, 1021.7 ,
1021.75, 1021.8 , 1021.85, 1021.9 , 1021.95, 1022. , 1022.05,
1022.1 , 1022.15, 1...
1027.7 , 1027.75, 1027.8 , 1027.85, 1027.9 , 1027.95, 1028. ,
1028.05, 1028.1 , 1028.15, 1028.2 , 1028.25, 1028.3 , 1028.35,
1028.4 , 1028.45, 1028.5 , 1028.55, 1028.6 , 1028.65, 1028.7 ,
1028.75, 1028.8 , 1028.85, 1028.9 , 1028.95, 1029. , 1029.05,
1029.1 , 1029.15, 1029.2 , 1029.25, 1029.3 , 1029.35, 1029.4 ,
1029.45, 1029.5 , 1029.55, 1029.6 , 1029.65, 1029.7 , 1029.75,
1029.8 , 1029.85, 1029.9 , 1029.95]),
scoring='neg_mean_absolute_percentage_error')[130]:
models['ridge']['MAPerE'] = model
alphas['MAPerE'] = model.alpha_
model.alpha_
[130]:
1024.2499999999961
[131]:
test_predictions = models['ridge']['MAPerE'].predict(X_test_scaled)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
MAPerE = metrics.mean_absolute_percentage_error(y_test, test_predictions)
errors['ridge']['MAPerE'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
r2=r2, MedAE=MedAE, MAPerE=MAPerE)
test_preds['ridge']['MAPerE'] = test_predictions
Analyzing error metrics#
[132]:
error_df = pd.DataFrame.from_dict(errors['ridge']).T
ndf = pd.concat([error_df, pd.Series(alphas.values(), index=alphas.keys(), name='alpha')], axis=1)
ndf.index.name = 'scoring'
ndf.columns.name = 'metric'
ndf
[132]:
| metric | MAE | MSE | RMSE | r2 | MedAE | MAPerE | alpha |
|---|---|---|---|---|---|---|---|
| scoring | |||||||
| MAE | 17968.776853 | 7.523634e+08 | 27429.243295 | 0.886246 | 12030.073612 | 0.108136 | 354.50 |
| MSE | 17800.404658 | 7.217229e+08 | 26864.900197 | 0.890878 | 12640.520799 | 0.108687 | 190.15 |
| RMSE | 17800.404658 | 7.217229e+08 | 26864.900197 | 0.890878 | 12640.520799 | 0.108687 | NaN |
| r2 | 17800.404658 | 7.217229e+08 | 26864.900197 | 0.890878 | 12640.520799 | 0.108687 | 190.15 |
| MedAE | 18385.122105 | 8.222842e+08 | 28675.498464 | 0.875674 | 11674.233991 | 0.108510 | 748.80 |
| MAPerE | 18686.683333 | 8.697449e+08 | 29491.437899 | 0.868498 | 12247.473170 | 0.109258 | 1024.25 |
Plotting error metrics#
Below is a plot of the error metric values as a function of the scoring metric that we used in the training step.
The acronyms are: - MAE: Mean Absolute Error - MSE: Mean Squared Error - RMSE: Root Mean Squared Error (not exactly using it as a scoring metric when training the model just wanted to make a better comparison to MAE) - r2: R Squared - MedAE: Median Absolute Error - MAPerE: Mean Absolute Percentage Error
[133]:
mapper = dict(MAE='Mean Absolute Error (MAE)', MSE='Mean Squared Error (MSE)',
RMSE='Root Mean Squared Error (RMSE)', r2='R Squared (r2)',
MedAE='Median Absolute Error (MedAE)',
MAPerE='Mean Absolute Percentage Error (MAPerE)')
# error_df.drop('MAPerE', axis=0, inplace=True)
# error_df.drop('MAPerE', axis=1, inplace=True)
fig, ax = plt.subplots(nrows=3, ncols=2, figsize=(9,8))
ax = np.ndarray.flatten(ax)
for i, col in enumerate(error_df.columns):
d = error_df[col]
ax[i].plot(d.index, d)
ax[i].set_title(mapper[col])
ax[i].set_xlabel('Scoring metric used when training')
fig.tight_layout()
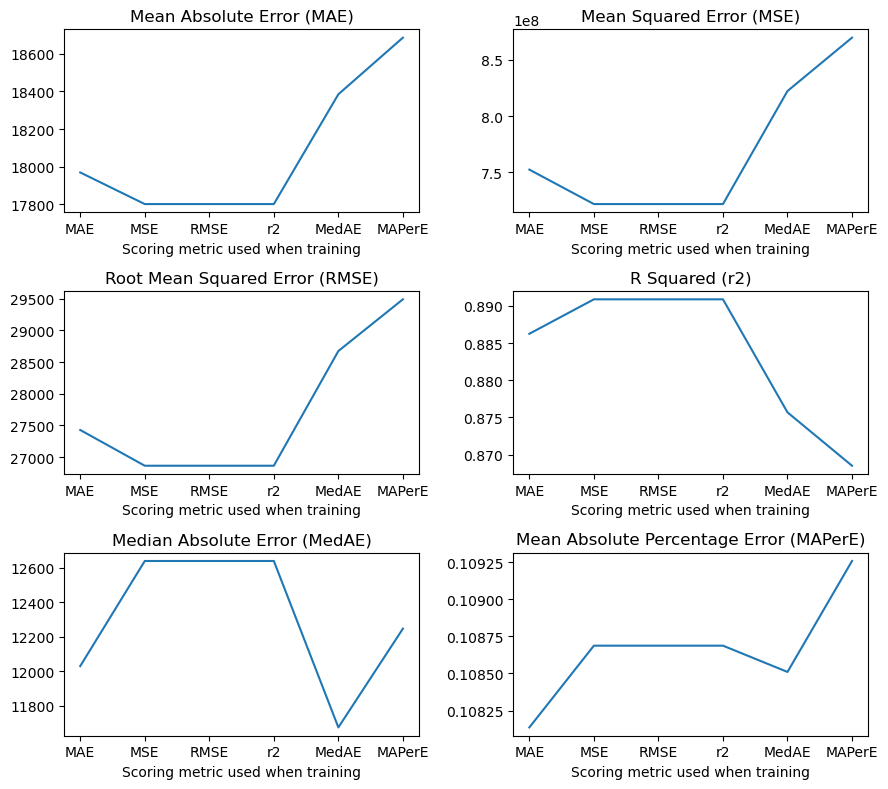
Plotting real vs. predicted values#
[134]:
fig, ax = plt.subplots(ncols=2, nrows=3, figsize=(10, 14))
ax = np.ndarray.flatten(ax)
base = int(np.floor(np.log10(y_test.mean())))
for idx, (key, value) in enumerate(test_preds['ridge'].items()):
str_vals = [convert_strings(y_test.mean(), base),
convert_strings(errors['ridge'][key]['MAE'], base),
convert_strings(errors['ridge'][key]['MedAE'], base),
convert_strings(errors['ridge'][key]['RMSE'], base),
errors['ridge'][key]['r2']]
sns.scatterplot(x=y_test, y=value, alpha=0.3, ax=ax[idx])
replace_price_ticks(ax[idx], True, 'Actual Sale Price / USD')
replace_price_ticks(ax[idx], False, 'Predicted Sale Price / USD')
xlim = ax[idx].get_xlim()
new_lim = list(ax[idx].get_ylim())
if new_lim[0] > xlim[0]: new_lim[0] = xlim[0]
if new_lim[1] < xlim[1]: new_lim[1] = xlim[1]
ax[idx].set_ylim(new_lim)
ax[idx].set_xlim(new_lim)
ax[idx].plot(new_lim, new_lim, color='tab:red', linestyle='--')
ax[idx].text(s='Scoring function\n{}\n'.format(mapper[key])+error_text.format(*str_vals), x=0.025, y=0.97,
transform=ax[idx].transAxes, ha='left', va='top',
bbox=dict(fc='none'))
fig.suptitle('Ridge Regression', fontsize=22)
fig.tight_layout()
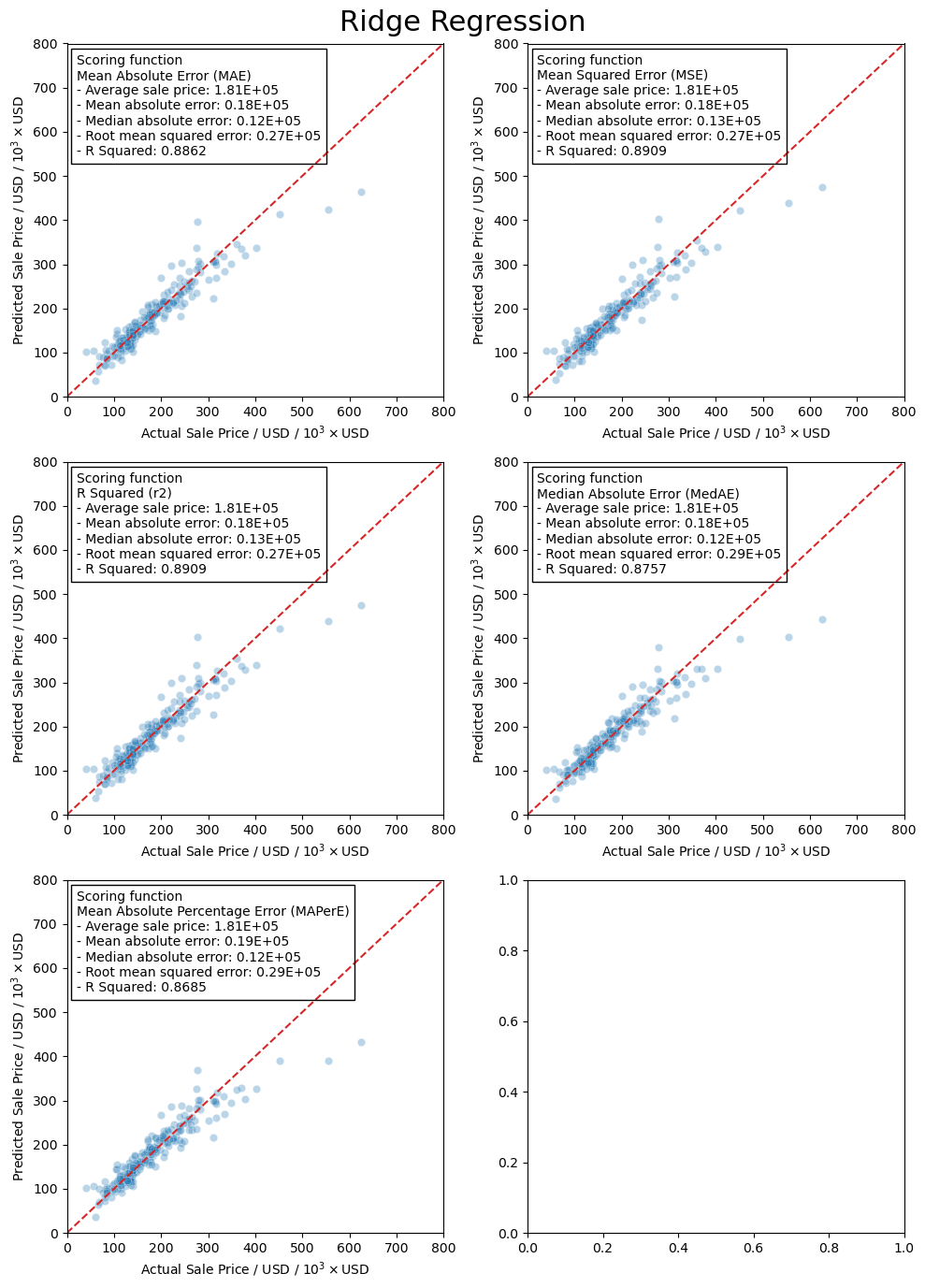
LASSO regression#
[135]:
model = LassoCV(n_alphas=1000, eps=0.001, max_iter=10000)
[136]:
model.fit(X_train_scaled, y_train)
[136]:
LassoCV(max_iter=10000, n_alphas=1000)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LassoCV(max_iter=10000, n_alphas=1000)
[137]:
models['lasso'] = model
model.alpha_
[137]:
342.5806017461771
[138]:
test_predictions = model.predict(X_test_scaled)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
MAPerE = metrics.mean_absolute_percentage_error(y_test, test_predictions)
test_preds['lasso'] = test_predictions
errors['lasso'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
MedAE=MedAE, r2=r2)
Plotting real vs. predicted values#
[139]:
fig, ax = plt.subplots()
gen_comp_plot('Lasso regression', test_predictions, y_test, ax,
avg_price, errors['lasso'])
fig.tight_layout()
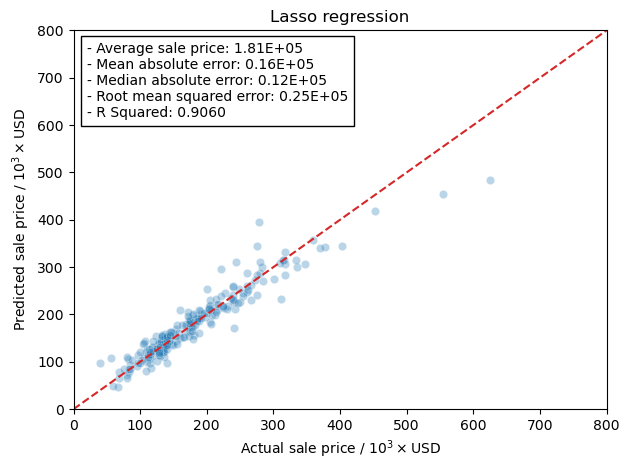
Elastic Net#
[140]:
model = ElasticNetCV(l1_ratio=np.arange(0.1, 1.1, 0.1), n_alphas=1000, eps=0.001, max_iter=int(1e5))
[141]:
model.fit(X_train_scaled, y_train)
[141]:
ElasticNetCV(l1_ratio=array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]),
max_iter=100000, n_alphas=1000)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ElasticNetCV(l1_ratio=array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]),
max_iter=100000, n_alphas=1000)[142]:
models['elastic'] = model
model.alpha_
[142]:
342.5806017461771
[143]:
model.l1_ratio_
[143]:
1.0
[144]:
test_predictions = models['elastic'].predict(X_test_scaled)
MAE = metrics.mean_absolute_error(y_test, test_predictions)
MSE = metrics.mean_squared_error(y_test, test_predictions)
RMSE = np.sqrt(MSE)
r2 = metrics.r2_score(y_test, test_predictions)
MedAE = metrics.median_absolute_error(y_test, test_predictions)
test_preds['elastic'] = test_predictions
errors['elastic'] = dict(MAE=MAE, MSE=MSE, RMSE=RMSE,
MedAE=MedAE, r2=r2)
Plotting real vs. predicted values#
[145]:
fig, ax = plt.subplots()
title = 'Elastic net / $\lambda={}$'.format(model.l1_ratio_)
gen_comp_plot(title, test_preds['elastic'], y_test, ax,
avg_price, errors['elastic'])
fig.tight_layout()
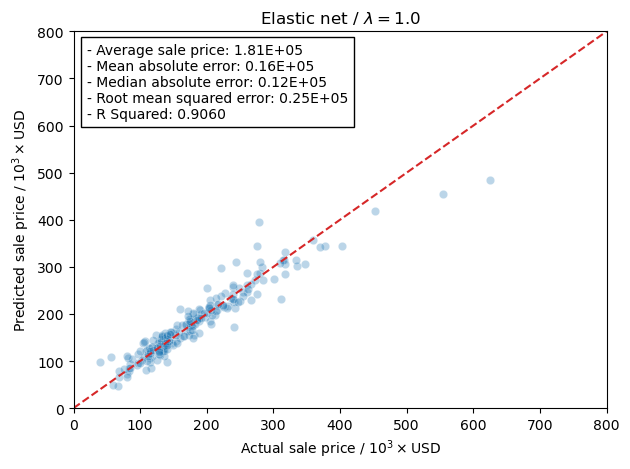
Conclusion#
First let’s put all of the models together with the plots of real vs. predicted in one large plot.
[146]:
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(10,10))
axs = np.ndarray.flatten(axs)
keys = ['ols', ['ridge', 'MAE'], 'lasso', 'elastic']
names = dict(ols='Ordinary Least Squares',
ridge='Ridge Regression',
lasso='LASSO regression',
elastic='Elastic Net')
for idx, (ax, key) in enumerate(zip(axs, keys)):
pred = test_preds[key] if not isinstance(key, list) else test_preds[key[0]][key[1]]
name = names[key] if not isinstance(key, list) else names[key[0]]
err = errors[key] if not isinstance(key, list) else errors[key[0]][key[1]]
if name.startswith('Elastic'):
name += ' / $\lambda={}$'.format(models['elastic'].l1_ratio_)
gen_comp_plot('', pred, y_test, ax, avg_price, err, text_tmp=name+'\n'+error_text)
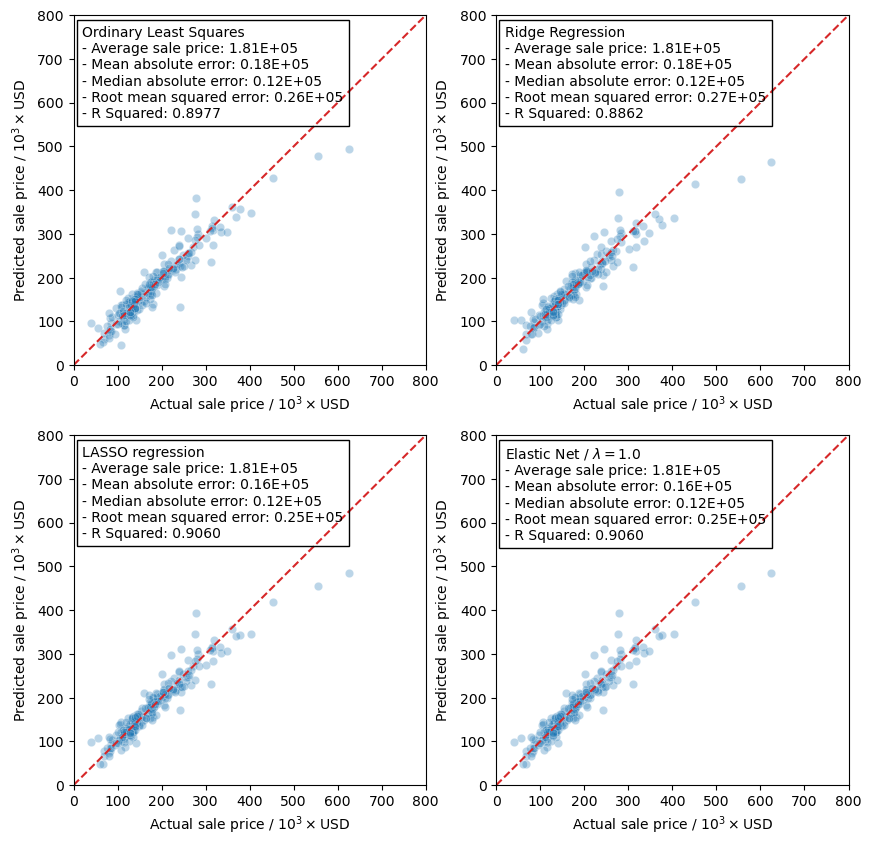
So what’s the final conclusion from all this. Well, it seems that the LASSO regression model actually gives the best predictions as it has the lowest error metrics and the best R squared value. This is further supported by the fact that the Elastic Net model prefers the LASSO regression model as it has a \(\lambda\) value of 1.0. Granted, all of the models actually seem to perform the same, and based on the results the use of any one of them in our test set should yield predictions with the same level of confidence.
What is interesting in this model, however, is that in our testing data we have the two points that are priced above 500,000. With the fitting parameters that we have it is possible that any predictions made above 500,000 may not be very accurate as they are not being included in the training data set. This could show a possible lack of data in that price range and possibly a lower confidence in the predictions.
[ ]: